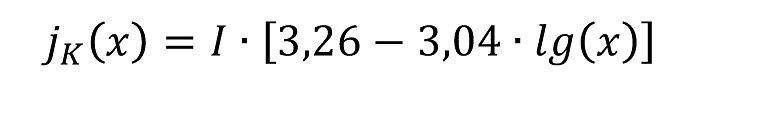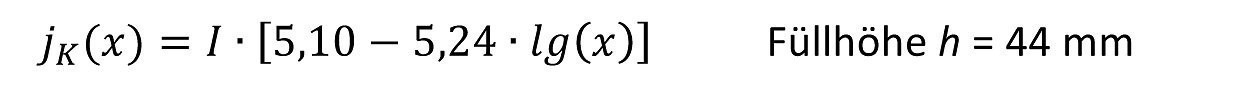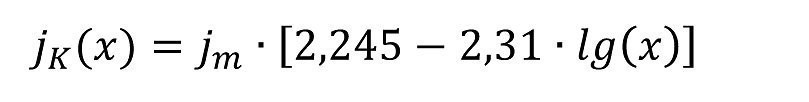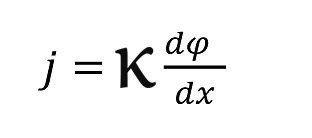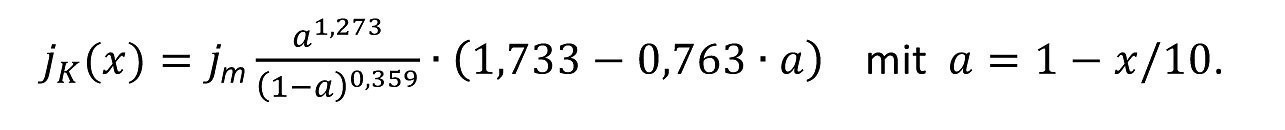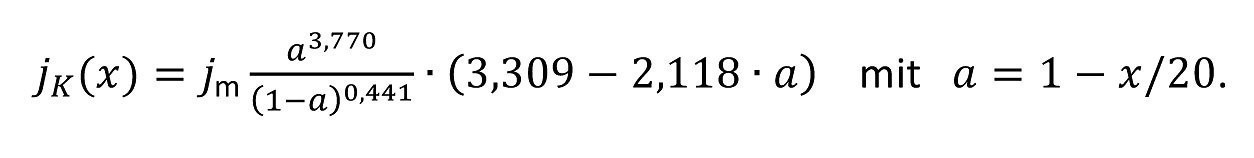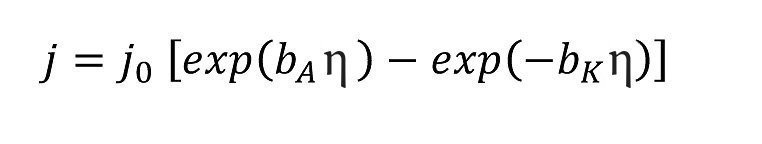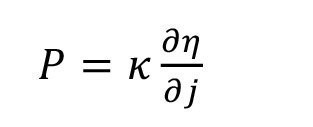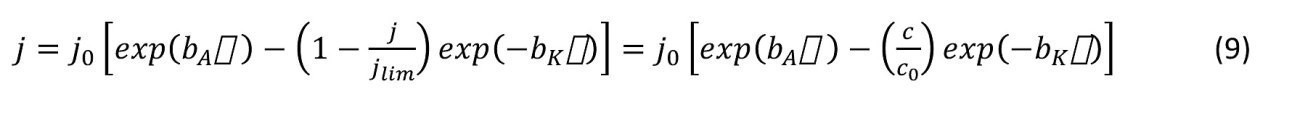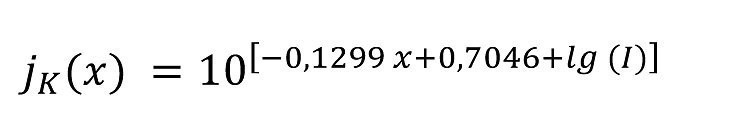1 Einleitung und Historie
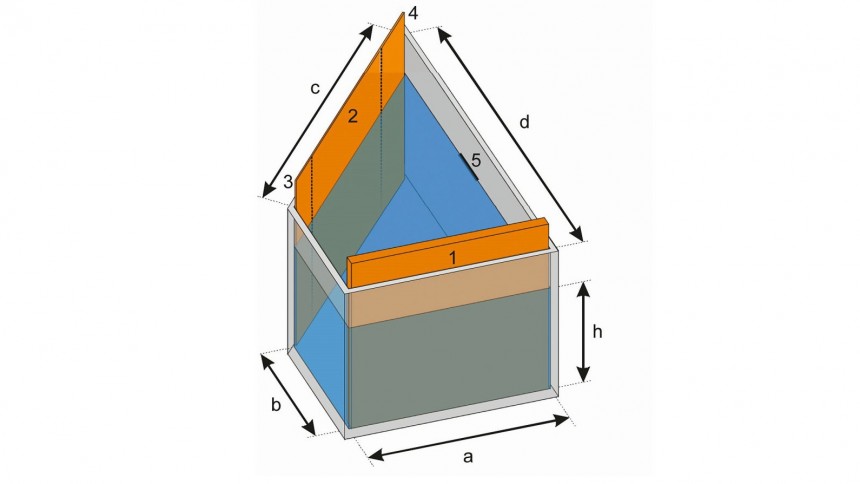
Die Verwendung von gewinkelten Elektrodenanordnungen geht auf Untersuchungen von Richard O. Hull zurück, weshalb die heute üblichen Zellen, siehe Abbildung 1, eng mit seinem Namen als Hull-Zellen verbunden sind [1]. Hull untersuchte die Stromdichteverteilung auf der Kathode (Elektrode 2 in Abb. 1) für verschiedene Systeme wie sauer Kupfer und Nickel sowie cyanidisch Zink und Cadmium. Die Ergebnisse fasste er in einer empirischen Zahlenwertgleichung zusammen, die im metrischen System folgende Form annimmt:
<1>
mit jK(x) lokale Stromdichte in A/dm2, / Strom in A, x lokaler Abstand des Blechs in cm zu Punkt 3, Elektrolytvolumen 1 L, Füllhöhe h = 44 mm.
Mit dieser Zelle sind sowohl qualitative als auch quantitative Beurteilungen von Elektrolyten möglich. In der Praxis hat sich besonders die schnelle Abschätzung des einsetzbaren Stromdichtebereichs durch die Bewertung der Optik der Überzüge als vorteilhaft erwiesen, sodass sie 1978 in eine entsprechende Norm (DIN 50957:1978, [2]) aufgenommen und um eine kleinere Variante mit einem Elektrolytvolumen von 250 mL ergänzt wurde. Für diese kleinere Zelle ergeben sich folgende Hull-Zellen-Gleichungen:
<2>
<3>
mit jm der mittleren Stromdichte in A/dm2, bei beliebiger Füllhöhe [3], wobei diese Gleichungen nur zwischen 1 cm und 8 cm von Markierung 3 (vgl. gestrichelte Linien in Abb. 1) gelten.
Ausgehend von diesen Gleichungen ist dann auch die Abschätzung der Schichtdickenverteilung und damit der (Makro-)Streufähigkeit möglich. Zusammenfassungen zur Hull-Zelle wurden von Nohse [4] sowie von Anderle und Jelinek [5] erarbeitet.
Mit der Zeit wurden diese Zellen weiterentwickelt, um sie an spezielle Bedürfnisse anzupassen. So entstanden noch kleinere Versionen (z.B. die „Tenori“-Zelle, 33 ml, [6]), welche an der TU Ilmenau für Untersuchungen in ionischen Flüssigkeiten verwendet wird sowie Lang-Zellen mit doppelter Kathodenlänge, die vor allem bei der alka- lischen Zink-Nickel-Abscheidung ihren Einsatz finden. Hinzu kommen rotierende zylindrische Hull-Zellen [7], um bei definierter Hydrodynamik die Streufähigkeit zu untersuchen. Dieser Weiterentwicklung wurde nun bei der periodischen Überarbeitung der Norm Rechnung getragen. Während die Original-Hull-Zelle (1 L) aus der Norm entfernt wurde, da sie praktisch nicht mehr verwendet wird, wurden eine Lang-Version sowie Kathodenbleche mit einer speziellen Winkelgeometrie in einen neuen Teil 2 aufgenommen. Um den Einfluss der Geometrieänderungen abschätzen und auch entsprechende Stromdichte-Ortskurven angeben zu können, wurden Simulationsrechnungen und Abscheideversuche durchgeführt.
| Dimensionen / mm | V / ml |
<) (cd) / ° |
|||||
|
a (Anode) |
b |
c* (Kathode) |
d |
h (Füllhöhe) |
|||
| Hull (DIN 1L) | 85 | 120 | 127 (125) | 212 | 1000 | 42.7 | |
| DIN(Standard) | 64 | 48 | 102 (100) | 127 | 44 | 250 | 39.0 |
| DIN-Lang | 64 | 60 | 202 (200) | 251 | 50 | 500 | 18.6 |
Tabelle 1 fasst die Dimensionen der historischen und neuen genormten Zellen zusammen.
2 Modellierung der Stromdichteverteilung
Auch wenn die Hull-Zelle ein einfaches System zu sein scheint, wird die Beschreibung ihrer Stromdichteverteilung (an der Kathode) schnell komplex. Zur Vereinfachung werden keine vor- oder nachgelagerten Reaktionen (z.B. die Ligandenabspaltung) sowie Nebenreaktionen (z.B. Wasserstoffentwicklung) oder Legierungsbildungen berücksichtigt. Dadurch kann die Zelle zweidimensional abgebildet werden (Sicht von oben), d.h., über die Elektrolythöhe treten keine Eigenschaftsänderungen auf.
Im Folgenden werden aufeinander aufbauende Modelle kurz diskutiert, und auch welche Vereinfachungen getroffen werden.
2.1 Primäre Stromdichteverteilung
In der einfachsten Beschreibung wird zunächst ein elektrisches Feld zwischen Anode (1) und Kathode (2) angelegt, wobei die Elektroden bündig an isolierte Wände angrenzen.
Die primäre Stromdichteverteilung ergibt sich dann aus dem elektrischen Feld der Elektrodengeometrie, wobei das elektrische Feld mit der Elektrolytleitfähigkeit κ skaliert. Es gilt das Ohm’sche Gesetz:
<4>
West, Matlosz und Landolt [8] haben mit der Christoffel-Transformation Gleichung <5> der primären Stromdichteverteilung auf der Kathode der Standard-Hull-Zelle abgeleitet:
<5>
Mit dem gleichen Vorgehen erhält man für die neue Lang-Zelle Gleichung <6>:
<6>
2.2 Sekundäre Stromdichteverteilung
In Abschnitt 2.1 wurden noch keine elektrochemischen Reaktionen berücksichtigt. Ihre Beschreibung erfolgt durch eine Form der Butler-Volmer-Gleichung (BV-Gleichung). Im Folgenden wird die konzentrationsunabhängige Form verwendet, welche Konzentrationsgradienten vor den Elektroden vernachlässigt und damit Diffusionsphänomene (und Konvektion) vernachlässigt:
<7>
mit j0 der Austauschstromdichte, bi den [A]nodischen und [K]athodischen Tafelfaktoren1 in V-1 und η der Polarisations- bzw. Überspannung. Die sekundäre Stromdichteverteilung ergibt sich dann aus dem Zusammenspiel zwischen Ohm’schem Widerstand und Polarisationswiderstand. Dies spiegelt der Polarisationsparameter P (in cm) wider Gleichung <8>, der erstmals von Hoar und Agar [9] erwähnt wurde:
<8>
Gegenüber der Wagner Zahl mit Wa = P/L (L charakteristische Länge) ist P unabhängig von der Geometrie und wird nur durch die Elektrolytkennwerte bestimmt. Je größer P umso gleichmäßiger ist die Schichtdickenverteilung, d.h. man benötigt eine hohe Elektrolytleitfähigkeit, um den Ohm’schen Widerstand gegenüber dem Polarisationswiderstand klein zu halten, bzw. umgekehrt einen großen Polarisationswiderstand. P ist direkt proportional zum inversen Anstieg der Stromdichte-Spannungs-Kurve (SPK) (Abb. 2). Der Anstieg der SPK sollte somit möglichst flach sein, damit der Polarisationsparameter groß und die Stromdichte- bzw. Schichtdickenverteilung gleichmäßiger werden, wie dies bei niedrigen Stromdichten sowie bei alkalischen Komplexbildner-haltigen Elektrolyten gegeben ist. Im Grenzstrombereich ist der Polarisationsfaktor zwar auch groß, jedoch erhält man hier pulvrige Abscheidungen, die meist unerwünscht sind.
Für die sekundäre Stromdichteverteilung ist ein System partieller Differentialgleichungen zu lösen, wobei die dabei auftretende Laplace-Gleichung nicht mehr analytisch sondern nur noch numerisch gelöst werden kann.
2.3 Tertiäre Stromdichteverteilung
Um die tertiäre Stromdichteverteilung zu erhalten, müssen im Unterschied zu Abschnitt 2.2 die Prozesse des Stofftransports wie Diffusion, Migration und Konvektion einbezogen werden. Insbesondere ist der Stofftransport in der Diffusionsschicht zu berücksichtigen, wobei hierfür die konzentrationsabhängige Form der Butler-Volmer-Gleichung <9> (hier nur für den kathodischen Teil) verwendet wird:
<9>
mit c Konzentration an der Elektrode, c0 Konzentration im Elektrolyten, jlim Grenzstromdichte. Mit Gleichung <9> wurde die idealisierte SPK in Abbildung 2 berechnet.
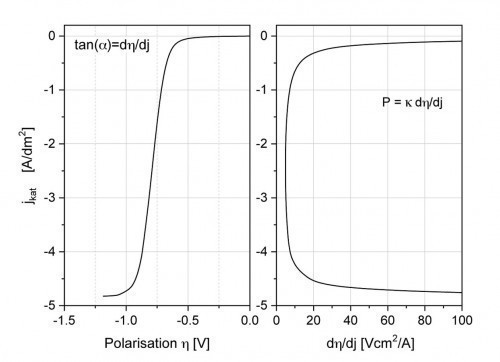 Abb. 2: Berechnete (idealisierte) Stromdichte-Spannungs-Kurve (links) und 1. Ableitung dη/dj (rechts)
Abb. 2: Berechnete (idealisierte) Stromdichte-Spannungs-Kurve (links) und 1. Ableitung dη/dj (rechts)
Im Rahmen dieses Beitrags wird nicht weiter auf die ter- tiäre Stromdichteverteilung eingegangen.
2.4 Simulationen
Wenn analytische Lösungen für die aufgestellten mathematischen Modelle (Gleichungen bzw. Gleichungssysteme) nicht mehr möglich sind, kommen numerische Verfahren zur Anwendung. Simulationsprogramme wie COMSOL Multiphysics® [10], Cell-Design® [11] oder Elsyca PlatingManager® [12] nutzen die Finite-Elemente-Methode (oder ähnliche Diskretisierungen) um Lösungen an Gitternetzpunkten zu erstellen, welche dann zu einem Gesamtbild zusammengesetzt und ausgewertet werden können. Ein Vorteil dieser Simulationen ist, dass man orts- und zeitaufgelöst Ergebnisse studieren kann, welche in der Realität nicht oder nur schwer zugänglich sind. Dazu kommt die Möglichkeit die Komplexität und Parameter frei variieren zu können. In Tabelle 2 sind die für die Simulationen verwendeten Werte angegeben, bei Abweichungen wird darauf hingewiesen.
|
Parameter |
Wert |
|
Elektrolytleitfähigkeit, κ |
0,1 S/cm |
|
Austauschstromdichte, j0 |
10-8 A/cm2 |
|
bK kathodischer Tafelfaktor |
39,0 V-1 |
|
Strom, I |
1 A |
3 Ergebnisse der Rechnungen und Simulationen
Prinzipiell zeigt sich, dass das Modell der primären Stromdichteverteilung der ungünstigste Fall für die Stromdichteverteilung ist. Wird das Modell durch Berücksichtigung der elektrochemischen Reaktionen komplexer angelegt, wird die Stromdichteverteilung an der Kathode gleichmäßiger. Für reale Systeme ist jedoch nicht immer ein komplexeres Modell zur Simulation notwendig, da die Verhältnisse der Parameter entscheidend sind. In Tabelle 3 sind einige Beispiele aufgeführt, mit denen die Streufähigkeit eines Elektrolyten bereits in vielen Fällen gut abgebildet werden kann.
Bei Simulationen können die Ergebnisse zudem Artefakte enthalten, die durch geometrische Details wie Netzauflösung an kleinen Strukturen (Ecken) oder Unstetigkeitsstellen (Randbereiche von elektrisch leitenden zu isolierenden Bereichen) entstehen. So steigt die Stromdichte an der Kante (Markierung 3) gegen unendlich, was in der Realität nicht der Fall ist.
3.1 Primäre und Sekundäre Feldverteilung in der Standard-Hull-Zelle
Die Simulationsergebnisse für die primäre und sekundäre Feldverteilung der Standard-Hull-Zelle sind in Abbildung 3 dargestellt. Sie zeigen sowohl die elektrische Feldverteilung (Äquipotentiallinien, Abb. 3a), als auch die daraus resultierenden Stromlinien (Abb. 3b) für beide Stromdichteverteilungen.
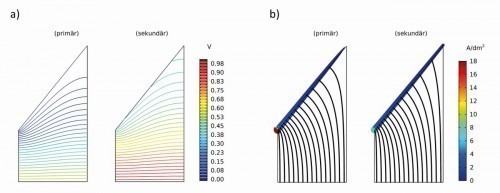 Abb. 3: Simulationsergebnisse für die Feldverteilung der Standard-Hull-Zelle, a) Äquipotentiallinien und b) Stromlinien und kathodische Stromdichte für (links) primäre und (rechts) sekundäre Feldverteilung
Abb. 3: Simulationsergebnisse für die Feldverteilung der Standard-Hull-Zelle, a) Äquipotentiallinien und b) Stromlinien und kathodische Stromdichte für (links) primäre und (rechts) sekundäre Feldverteilung
Bei der sekundären Feldverteilung (Abb. 3a rechts) verlaufen die Äquipotentiallinien weitgehend parallel zur Anode, auch in der spitzen Ecke der Zelle; während sie sich bei der primären Feldverteilung kurz vor dem Ende von Seite b (siehe Abb. 1) langsam drehen und sich fast parallel zur Kathode ausrichten. Damit kommt es zu einer starken Bündelung der Stromlinien auf den Beginn der Kathode nahe dem Markierungspunkt 3 (Abb. 3b). Bei der sekundären Feldverteilung gibt es hingegen nur eine leichte Krümmung der Stromlinien, so dass die Stromdichteverteilung auf der Kathode deutlich gleichmäßiger ist, was in diesem Fall die bessere Streufähigkeit erklärt. Abschnitt 3.4 geht auf einige Praxisbeispiele für beide Situationen ein.
3.2 Primäre Stromdichteverteilung der Standard-Hull-Zelle und der Lang-Zelle
In Abbildung 4a und b sind die lokalen Stromdichteverläufe jK(x) in Abhängigkeit von der Position x auf dem Kathodenblech entsprechend den Gleichungen <2>, <5> und <6> sowie der Simulation dargestellt.
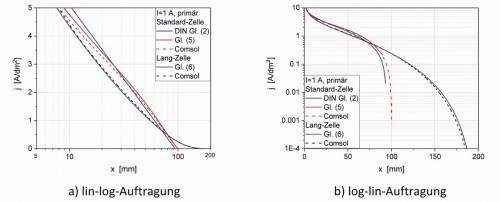 Abb. 4: Primäre kathodische Stromdichteverteilung der Standard-Hull-Zelle (mit I = 1 A, d. h. jm = 2,27 A/dm2) und der Lang-Zelle (mit I = 1 A, d. h. jm = 1,0 A/dm2)
Abb. 4: Primäre kathodische Stromdichteverteilung der Standard-Hull-Zelle (mit I = 1 A, d. h. jm = 2,27 A/dm2) und der Lang-Zelle (mit I = 1 A, d. h. jm = 1,0 A/dm2)
Mit einer logarithmischen Längenachse (Abb. 4a) ergibt sich für die Standard-Hull-Zelle nach Gleichung <2> (blaue Kurve) ein linearer Kurvenverlauf mit einem Schnittpunkt durch die x-Achse bei 9 cm, während er für Gleichung <5> nach [8] (rote Kurve) nur annähernd linear ist. Einen ähnlichen Verlauf zeigt die COMSOL-Simulation (rot gestrichelte Kurve).
In Abbildung 4b mit einer logarithmischen Stromdichteachse sieht man deutlicher die Effekte an den Kanten: starker Stromdichteanstieg an Punkt 3 (bei x = 0 mm) bzw. starke Abnahme an Punkt 4 (x = 100 mm). Auch die Kurve für die Simulation zeigt wiederum bis auf kleine Abweichungen eine Übereinstimmung zu Gleichung <2> und <5> im Bereich 1 ≤ x/cm ≤ 8, so dass die geringen Unterschiede für die experimentellen Untersuchungen keine Rolle spielen. Damit wird auch klar, dass die von Hull vorgeschlagenen Gleichungen im Wesentlichen den primären Stromdichteverlauf widerspiegeln.
Prinzipiell ähnlich ist das Bild für die Lang-Zelle, wobei hier auffällt, dass sich nahezu der gesamte Strom auf die ersten ca. 80 mm der verlängerten Kathode konzentriert. Ab ca. 120 mm kommt es zu einem wachsenden Einbruch der Stromdichte. Für die Lang-Zelle zeigen die Kurven ebenfalls eine gute Übereinstimmung zwischen der Simulation und Gleichung <6>. Aber weder in der lin-log- noch in der log-lin-Darstellung tritt ein linearer Bereich auf (näherungsweise nur linear zwischen 10–80 mm).
Die geringeren Stromdichten der Lang-Zelle im Vergleich zur Standard-Zelle in Abbildung 4 sind auf die geringere mittlere Stromdichte zurückzuführen.
3.3 Sekundäre Stromdichte-Verteilung der Lang-Zelle
Weiterhin wurde die Simulation der sekundären Stromdichte-Verteilung untersucht. Abbildung 5 zeigt die Ergebnisse der Lang-Zelle. Für die Standard-Hull-Zelle sei auf Abschnitt 4.2 (Abb. 9) verwiesen.
Während sich im hohen Stromdichtebereich (x ≤ 100 mm) kaum Änderungen ergeben, bricht die Stromdichte in der zweiten Hälfte des Blechs nicht mehr so drastisch ein, sondern fällt weiter linear bis kurz vor das Ende ab (Abb. 5a). Über einen Großteil des Bleches (1 ≤ x/cm ≤ 19) kann der Verlauf der Stromdichte mit folgender Gleichung annähernd beschrieben werden Gleichung <A.3> in [3]:
<10>
wobei lg (1) bei einer Füllhöhe von 50 mm auch durch lg (j) ersetzt werden kann. Damit konzentriert sich der Strom zwar weiterhin auf die erste Hälfte mit einem linearen Abfall identisch zur primären Stromdichte-Verteilung, in der zweiten Hälfte ist der Stromdichte-Abfall jedoch nicht mehr so stark wie bei der primären Stromdichte-Verteilung. Die Makrostreufähigkeit verbessert sich somit deutlich von der primären zur sekundären Stromdichte-Verteilung (vgl. Abschnitt 2 und Anfang dieses Abschnitts 3).
3.3 Variation kinetischer Parameter am Beispiel der Lang-Zelle
In Tabelle 2 wurden die Parameter für die bisherigen Berechnungen angegeben. Die praktischen Werte weichen aber je nach Metall und Elektrolyt von diesen Werten teilweise beträchtlich ab.
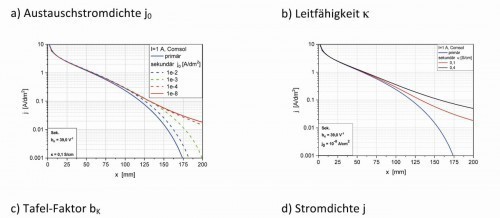
Simulationen bieten die Möglichkeit, durch eine gezielte Änderung der Parameter den Einfluss dieser auf das Gesamtsystem zu bestimmen. Hierzu wurden die kinetischen Parameter j0, bK, κ und I bzw. jm variiert (Abb. 6).
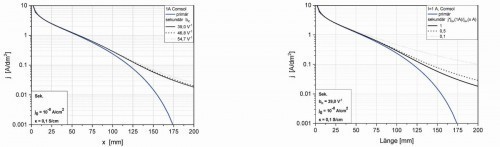 Abb. 6: Variationen der Parameter: a) j0, b) κ, c) bK und d) j
Abb. 6: Variationen der Parameter: a) j0, b) κ, c) bK und d) j
Es zeigt sich, dass vor allem das Verhältnis zwischen Elektrolytleitfähigkeit und Polarisation bzw. Überspannung über die Stromdichteverteilung entscheidet. Variiert man die Austauschstromdichte, so erhält man bei großem j0 eine primäre und bei kleinen Werten entsprechend eher eine sekundäre Stromdichteverteilung (Abbi. 6a), da große Austauschstromdichten zu einer kleinen Polarisation und damit einer steilen SPK (kleinerer P) führen (vgl. Gl. <8> und Abb. 2). Ändert man die Leitfähigkeit, so erhält man bei hohen Werten (großer P) eine sekundäre, bei kleineren Werten eine primäre Verteilung (Abb. 6b). Während der Tafel-Faktor nur geringe Auswirkungen auf P und damit auf die sekundäre Stromdichteverteilung hat (Abb. 6c, nur eine in der Praxis kaum auftretende Vergrößerung von bK auf Werte > 60 V-1 vergleichmäßigen die Stromdichte-Verteilung), ist auch die Wahl des angelegten Stroms entscheidend (Abb. 6d). Je kleiner der angelegte Strom (die mittlere Stromdichte) ist, desto flacher wird die Kurve der Stromdichteverteilung. In Abbildung 2 ist das deutlich an dem flacheren Verlauf der Stromdichte-Potential-Kurve zu erkennen. Es sei hier noch einmal darauf hingewiesen, dass es in realen Systemen durch zusätzliche vor- oder nachgelagerte Reaktionen und damit verbundener Reaktionsüberspannungen zu weiteren Abweichungen der Stromdichteverteilung gegenüber der einfachen BV-Gleichung kommen kann.
3.4 Vergleich mit experimentellen Ergebnissen
In der praktischen Anwendung der Hull-Zellen hat sich schon gezeigt, dass je nach Metallabscheidung Abweichungen der Stromdichteverteilung zu den Gleichungen <2>, <5>, <6> und <10> sowie zur Simulation auftreten. Das ist auch nicht verwunderlich, da diese Gleichungen im Wesentlichen die primäre Stromdichte-Verteilung bzw. die sekundäre mit der einfachen BV-Gleichung abbilden (Kapitel 3). Dabei ist für die Lang-Zelle zu berücksichtigen, dass hier nur experimentelle Daten für ähnliche Zellen vorliegen, wobei sich aber keine wesentlichen Unterschiede zur standardisierten Geometrie zeigten (siehe auch Kapitel 4).
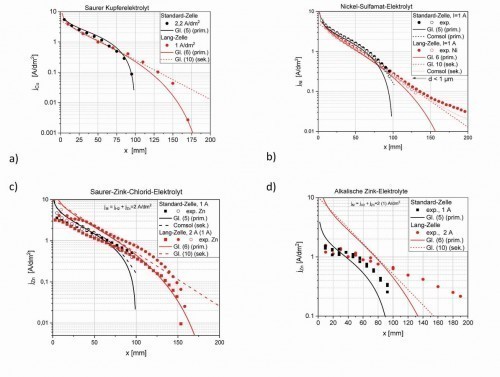
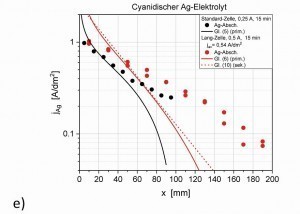 Abb. 7: Vergleich der Simulationen mit realen Systemen: a) sauer Kupfer, b) Sulfamat-Nickel, c) sauer Zink, d) alkalisch Zink und e) cyanidisch Silber
Abb. 7: Vergleich der Simulationen mit realen Systemen: a) sauer Kupfer, b) Sulfamat-Nickel, c) sauer Zink, d) alkalisch Zink und e) cyanidisch Silber
Die Ermittlung der lokalen Stromdichte erfolgte über Schichtdickenmessungen mittels RFA in einem 2 cm breiten Streifen in der Mitte der beschichteten Fläche analog DIN 50957-1 und -2. Insbesondere ist dabei zu berücksichtigen, dass im niedrigen Stromdichtebereich die Schichtdicken unter 1 µm liegen und damit der Fehler der Messung bzw. der daraus berechneten Stromdichten ansteigt. Der Vergleich zwischen den Experimenten und den Gleichungen bzw. Simulationen ist sowohl für die Lang-Zelle als auch die Standard-Hull-Zelle in Abbildung 7 zusammengestellt. Tabelle 3 (siehe unten) stellt die Streufähigkeit und das notwendige Simulationsmodell für die untersuchten Systeme gegenüber.
|
System |
Stromdichte- verteilung und Modellierung |
Streufähigkeit |
|
sauer Cu |
primär |
schlecht |
|
sauer Ni |
sekundär |
gut |
|
cyan. Ag alkalisch ZN |
tertiär |
sehr gut |
Sauer Kupfer
Abbildung 7a zeigt experimentelle Daten von Abscheidungen in der Standard-Hull- und Lang-Zelle. Die Abscheidung konzentriert sich auf den Anfang der Kathode, auch bei der langen Zelle. Die sehr gute Übereinstimmung mit den entsprechenden Kurven für die primäre Stromdichte-Verteilung (Gl. <6>) lässt den Schluss zu, dass diese für die Charakterisierung des Systems ausreichend ist. Der Grund dafür ist die relativ geringe Polarisation bei einer großen Austauschstromdichte von j0 = 3×10-4 A/cm2, die einige Zehnerpotenzen größer ist als die in Tabelle 1 angegebene [13].
Sulfamat-Nickel
Die in Abbildung 7b gezeigten experimentellen Daten der Nickelabscheidung stimmen gut mit Gleichung <10> überein. Somit kann dieses System mit der sekundären Stromdichte-Verteilung beschrieben werden, obwohl die Wasserstoffentwicklung in der theoretischen Kurve nicht berücksichtigt wurde2. Die Streufähigkeit ist deutlich besser. Insbesondere zeigt sich bei der Nickelabscheidung nicht der große Schichtdickenabfall wie bei der Kupferabscheidung im niedrigen Stromdichte-Bereich, wobei dort kleinere Zellströme zu relativ höheren Stromdichten führen. Im oberen Stromdichte-Bereich ergibt sich dagegen auch eine Annäherung an die primäre Verteilung. Auch bei der Nickelabscheidung konzentriert sich der Strom auf die ersten 10 cm der Fläche.
2 Prinzipiell können in Simulationen auch weitere Reaktionen berücksichtigt werden. Im Fall von Nickel traten aufgrund der hohen Stromausbeute keine signifikanten Unterschiede hinsichtlich der Simulation mit oder ohne Wasserstoff auf. Deshalb wurde hier auf die Darstellung dieser Simulationsergebnisse verzichtet.
Sauer Zink
Ein kommerzieller saurer Zink-Elektrolyt zeigt in den Experimenten weitgehend sowohl bei einem Strom von 1 bzw. 2 A ein Verhalten, welches der primären Stromdichteverteilung gleicht (Abb. 7c). Der Stromdichteverlauf scheint im Vergleich zur oben angegebenen Simulation, Gleichung <10>, und zu Gleichung <6> etwas flacher zu sein und bricht dann ein. Für additivfreie Elektrolyte ist die Austauschstromdichte der Zinkabscheidung mit j0 = 5 10×10-2 A/cm2 ebenfalls sehr hoch [14].
In der Standard-Hull-Zelle ist dagegen jedoch kein Einbruch im niedrigen Stromdichte-Bereich zu erkennen, so dass die Lang-Zelle den unteren Stromdichte-Bereich in diesem Fall wesentlich spreizt.
Für diese drei Systeme ergeben sich kaum Vorteile der Lang-Zelle gegenüber der Standard-Hull-Zelle. Der Bereich ab 10 cm liefert keine neuen Informationen.
Alkalisch Zink und Cyanidisch Silber
Ein völlig anderes Verhalten tritt bei komplexierten Elektrolyten auf. Die bisher angegebenen Gleichungen <3>, <5>, <6> oder <10> für beide Zelltypen und für eine Elektrodenreaktion sind für diese Abscheidungsprozesse nicht anwendbar. Abbildung 7d zeigt dies für alkalische Zink-Elektrolyte, wobei die Metallabscheidung aus der Entladung der Hydroxo-Zink-Komplexe nicht nur mit wesentlich größeren Überspannungen stattfindet, sondern auch mit einer stärkeren Wasserstoffentwicklung verbunden ist als im Fall von sauren Nickel-Elektrolyten. Die experimentellen Daten zeigen einen deutlich flacheren bzw. gleichmäßigeren Verlauf der Stromdichte gegenüber der Kathodenlänge im Vergleich zu den Gleichungen <6> oder <10>, der starke Abfall der Stromdichte ab der Mitte der Kathode tritt hier nicht auf. Für cyanidische Silberelektrolyte ergaben sich vergleichbare Ergebnisse (Abb. 7e)
.In diesen beiden Fällen kommt es damit bei der Lang-Zelle zu einer Spreizung des Stromdichtebereichs über die verlängerte Kathode und man erhält auch signifikante Stromdichten im unteren Stromdichtebereich. Hinsichtlich der Simulation des Abscheidungsprozesses müssen zusätzlich die Reaktionen der Komplexe und insbesondere damit verbundene Diffusionsprozesse berücksichtigt werden.
4 Einfluss der Geometrie
Neben der Variation kinetischer Parameter (vgl. Abschnitt 3.3) ist es mit Simulationen auch schnell möglich, andere Geometrien zu charakterisieren. Im Folgenden werden kurz die Verschiebung der Anode am Beispiel der Standard-Hull-Zelle sowie die Verbreiterung bzw. Verschmälerung der beiden normierten Zellen besprochen.
4.1 Verschiebung der Anode und primäre Feldverteilung
Im Rahmen des Entwurfs der DIN wurde insbesondere auch die Frage diskutiert, wie dick die Anode sein darf, um den Kathoden-Anoden-Abstand als Einflussgröße auszuschließen. Dazu wurden Simulationen zur primären Stromdichte-Verteilung durchgeführt, wobei die Anode um einen Betrag dy in Richtung Kathode oder von ihr weg verschoben wurde, siehe Abbildung 8, wobei dy < 0 einer Verringerung des Anoden-Kathoden-Abstands entspricht. Wie zu erwarten, nimmt die Zellspannung mit zunehmendem Abstand aufgrund des Elektrolytwiderstands zu (a–c), während sich der Verlauf der Stromlinien praktisch nicht verändert. Sie bleiben im rechtwinkligen Teil der Zelle weitgehend parallel und verbiegen sich erst kurz vor der Kathode. Die entsprechenden kathodischen Stromdichten sind in Abbildung 8d gezeigt und liegen so eng beieinander, dass sie als identisch angesehen werden können, auch im Vergleich zu Gleichungen<(2> und <5>. Erst bei starker Annäherung von Anode und Kathode (b ≤ 10 mm) kann es zu Veränderungen in der Stromdichteverteilung kommen (Abb. 8d, dy = -38,4 mm).
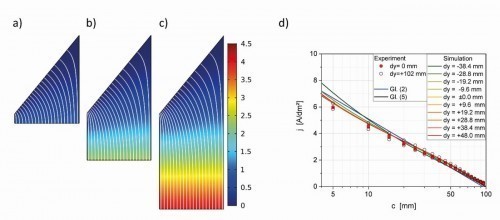 Abb. 8: Simulierte primäre Feldverteilung und Stromlinien für a) eine verkürzte (dy = -38.4 mm), b) normal-lange (dy = 0.0 mm) und c) verlängerte (dy = +48.0 mm) Hull-Zelle sowie d) die Stromdichte- verteilungen auf der Kathode als Funktion von dy im Vergleich zur Nickelabscheidung mit dy = 0 und 102 mm
Abb. 8: Simulierte primäre Feldverteilung und Stromlinien für a) eine verkürzte (dy = -38.4 mm), b) normal-lange (dy = 0.0 mm) und c) verlängerte (dy = +48.0 mm) Hull-Zelle sowie d) die Stromdichte- verteilungen auf der Kathode als Funktion von dy im Vergleich zur Nickelabscheidung mit dy = 0 und 102 mm
Experimentell wurde dies mit der Nickelabscheidung mit einer modifizierten Zelle (dy = 102 mm, b = 150 mm) verifiziert, siehe Abbildung 8d. Dabei konnten keine Unterschiede zwischen beiden Zellen festgestellt werden.
Damit ist eine Variation der Anodendicke von 1-5 mm durchaus vertretbar, so dass selbst eine 10 mm starke Anode ohne Bedenken eingesetzt werden kann.
Auf den ersten Blick mag der Effekt etwas überraschend erscheinen, dass der Kathoden-Anoden-Abstand kaum eine Rolle spielt und manche Praktiker erwarten mit größerem Abstand eine gleichmäßigere Stromdichte-Verteilung. Das ist aber in diesem Fall auf die homogene Feldverteilung mit dem Ausfüllen des kompletten Volumens zurückzuführen, und der Einfluss des Polarisationswiderstands zeigt sich erst an der Elektrode.
Letztendlich ist dieser Effekt auch auf die Lang-Zelle übertragbar.
Unabhängig von den Original-Maßen der DIN 50957-2 wird im Anhang B zusätzlich eine weitere Lang-Zelle von der Firma Yamamoto „Japan-Zelle“ [3, 6] beschrieben. Diese Lang-Zelle ist von den Maßen her etwas kürzer, d.h., die beiden Seiten b und d (vgl. Abb. 1) sind 12 mm kürzer, wodurch sich der Kathoden-Anoden-Abstand verringert. Die Simulationen zeigten auch hier keine signifikanten Unterschiede hinsichtlich der primären und sekundären Stromdichte-Verteilung, so dass auch in der Praxis beide Zellen gleichwertig eingesetzt werden können.
4.2 Variation der Breite von Standard-und Lang-Hull-Zelle
Eine geometrische Alternative zur nun normierten Lang-Zelle wäre gewesen, die Standard-Zelle zu verbreitern und dafür die Winkel unverändert zu lassen. Eine solche Zelle hätte die Dimensionen: a = 128 mm, b = 48 mm, c = 202 mm, d = 206 mm und h = 44 mm. Aufgrund der doppelten Fläche müsste dann auch der Strom verdoppelt werden (I = 1 bzw. 2 A). Abbildung 9a und b zeigen den Vergleich der sekundären Stromdichteverteilung einer solcherart verbreiterten Zelle mit der Standard-Hull-Zelle. Als x-Achse ist in diesem Fall die relative Länge der Kathode x/c gewählt. Geht man den umgekehrten Weg bei der Lang-Zelle zu einer schmaleren Zelle (a = 32 mm, b = 60 mm, c = 102 mm, d = 156 mm und h = 50 mm), so erhält man die Kurven in Abbildung 9c und d (I = 0,5 bzw. 1 A).
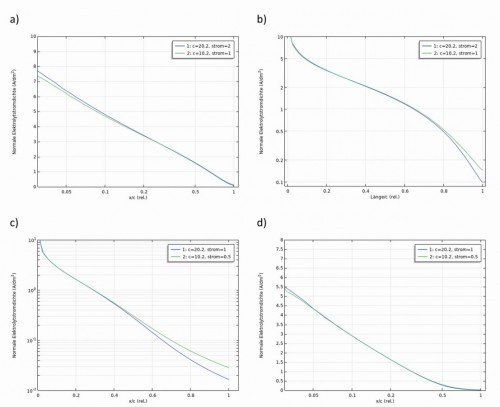 Abb. 9: Vergleich der simulierten sekundären Stromdichteverteilungen der (grün) Standard-Hull-Zelle und einer (blau) verbreiterten Version in a) lin-log-Darstellung, b) in log-lin-Darstellung sowie einer (blau) normalen Lang-Hull-Zelle und einer (grün) schmaleren Version c) und d)
Abb. 9: Vergleich der simulierten sekundären Stromdichteverteilungen der (grün) Standard-Hull-Zelle und einer (blau) verbreiterten Version in a) lin-log-Darstellung, b) in log-lin-Darstellung sowie einer (blau) normalen Lang-Hull-Zelle und einer (grün) schmaleren Version c) und d)
Für beide Versionen fallen die Kurven unter Verwendung relativer Längen (x/c) übereinander. Daraus folgt, dass die Stromdichte-Verteilungen bei Winkel-ähnlichen Geometrien mit der Kathodenlänge (bzw. -fläche) und gleicher mittlerer Stromdichte skaliert werden. Somit können auf einfache Weise auch die Stromdichte-Verläufe für ähnliche Zellen, wie z.B. der „Tenori“-Zelle aufgestellt werden [6].
Für die vorgeschlagenen Geometrien gibt es bisher keine experimentellen Untersuchungen, so dass sich erst noch zeigen muss, ob solche Zellen einen Nutzen haben oder andere Vorteile bieten.
5 Zusammenfassung
Im Rahmen der Überarbeitung der DIN 50957 wurden zweidimensionale Simulationsrechnungen der Standard Hull- (250mL) und der neuen Lang-Zelle sowie weiterer Geometrien durchgeführt. Dabei wurden nur einfache Reaktionen unter primären oder sekundären Feldverteilungen berücksichtigt.
Die simulierten primären Stromdichteverteilungen stimmen gut mit den aus der Literatur bekannten analytischen Lösungen überein. Im Falle der Standard-Hull-Zelle gilt dies auch für die traditionelle Hull-Gleichung, so dass diese eindeutig eine mittlere primäre Feldverteilung beschreibt.
Großen Einfluss auf die Stromdichteverteilung haben die Elektrolytleitfähigkeit, die Austauschstromdichte, der angelegte Strom und der spitze Winkel der Zelle. Hohe Elektrolytwiderstände, Austauschstromdichten und Ströme favorisieren eine primäre Stromdichte-Verteilung und damit schlechte Streufähigkeiten. Dagegen hat die Länge des rechteckigen Teils der Hull-Zelle (Seite b in Abb. 1) keinen Einfluss auf die Stromdichteverteilung, solange ein Mindestabstand gewahrt bleibt.
Experimentell kann das primäre Feldverhalten am besten bei der sauren Kupfer-Abscheidung beobachtet werden. Die sekundäre Stromdichteverteilung führt zu einer gleichmäßigeren Stromdichteverteilung, wie sie z.B. bei Nickel-Abscheidungen auftritt. Damit können diese Systeme gut mit dem Modell und den entsprechenden Parametern angepasst werden. Alkalische (und cyanidische) Systeme können mit diesen Simulationen nur unzureichend beschrieben werden.
Der Vergleich zwischen Standard-Hull- und Lang-Zelle zeigt, dass die Änderung des Winkels zu einer Verzerrung der Stromdichteverteilung führt, aber nicht zu einer Spreizung der Stromdichteverteilung. Bei komplexierten Systemen führen Reaktionsüberspannungen zu einer deutlichen Abflachung und Spreizung der Stromdichteverteilung. Für diese Fälle bietet die Lang-Zelle deutliche Vorteile. Hinsichtlich der Simulation erfordert das aber eine Erweiterung des Abscheidungsmodells unter Berücksichtigung des komplexeren Abscheidungsmechanismus zur Berechnung der Stromdichte-Verteilung.
Die in [3] angegebenen Winkelkathoden erfordern eine dreidimensionale Simulation. Dieser Fall soll in einem weiterführenden Artikel diskutiert werden.
Danksagung
Für hilfreiche Diskussionen sowie experimentelle Untersuchungen danken die Autoren unseren jetzigen und ehemaligen Mitarbeitern bzw. Studenten des Fachbereichs Elektrochemie und Galvanotechnik der TU Ilmenau insbesondere Dr. rer. nat. C. Kubeil, Frau M. Lerp, Frau Dr.-Ing. C. A. Vlaic, Frau N. A. Binti Omar und Frau S. Schorn sowie den Herren Dr.-Ing. C. Baumer, C. Mösle, M. Fritz, M. Leimbach und C. Tschaar sowie W. Yamamoto, Dr.-Ing. habil. U. Pilz und Dr. rer. nat. J. Herrmann.
Unser Dank gilt auch den beteiligten Kollegen vom DIN-Ausschuss, den Herren N. Distelrath und Dr. S. Gerhold sowie R. Paulsen, R. Krauß und R. Gensicke.
LITERATUR
[1] R.O. Hull; Proc. Am. Electroplater’s Soc. 27 (1939), 52
[2] DIN 50957:1978
[3] DIN50957-1:2016 und -2:2019
[4] W. Nohse: Die Untersuchung galvanischer Bäder in der Hull-Zelle, Eugen G. Leuze-Verlag, Bad Saulgau, 1987
[5] C. Anderle; T.W. Jelinek: Hull-Zelle zur Untersuchung von galvanischen Elektrolyten, Eugen G. Leuze Verlag, Bad Saulgau, 2007
[6] Firmenschrift (Katalog) von Yamamoto-MS Co., LTD, Tokyo, Japan
[7] C.T.J. Low; C. Ponce de Leon et al.: Aus. J. Chem. 58(4) (2005), 246
[8] A.C. West; M. Matlosz; D. Landolt: J. Appl. Electrochem. 22 (1992), 301
[9] T.P. Hoar; J.N. Agar: Discussions Faraday Soc. 1 (1947), 162
[10] COMSOL Multiphysics®, COMSOL AB, Stockholm, Schweden
[11] CELL-DESIGN®, Software for Computer Aided Design and Simulation of Electrochemical Cells, L-Chem, Inc., Shaker Heights, OH, USA
[12] Elsyca PlatingManager®, Elsyca® NV, Wijgmaal (Leuven), Belgium
[13] V.S. Donepudi; R. Venkatachalapathy; P.O. Ozemoyah; C.S. Johnson; J. Prakash: Electrochemical and Solid-State Letters, 4(2) (2001), C13
[14] H. Sierra Alcazar; J. Harrison: Electrochim. Acta 22 (1977), 627