Galvanic deposition = electrochemical transport?

Electroplating has been practiced for 221 years since the invention of the Voltaic column. In terms of large-scale technology, it has been 154 years since the invention of the dynamo machine by Werner von Siemens in 1867. Due to its direct application, electroplating has always been a domain of craftsmanship and technology in the most positive sense. After all, it is an art and a question of a great deal of practical experience and intuition to "correctly" coat objects with their various defects and inhomogeneities. In this context, it is a pleasure to read the practical literature, as it shows how profound the heuristics in this field are. As an advocate of "both and", it is important for me to make it clear in this introduction that an academic view and approach would not be fundamentally superior or even sufficient on its own to achieve good results in practice (!).

Too often, the history of technologies in the field of tension between empiricism and science is presented in a one-sided and distorted way. In electroplating, however, there is no reason for this. In order to fully comprehend or even understand an issue, whether it is of a practical or theoretical nature, it is necessary to look at it from as many angles as possible, ideally from all accessible perspectives and from all directions. It is particularly interesting to see how differently various scientific and technical disciplines approach one and the same issue. From the inside, i.e. from the respective discipline alone, the picture often and erroneously appears complete, while other approaches tend to reveal the respective epistemological flaws, albeit never completely.

In this article, I would like to take a closer look at a parallel I have noticed, namely between electrodeposition and chemical transport, which leads me to the conclusion that electrodeposition should be described as electrochemical transport.

First of all, the term chemical transport, coined by the famous German chemist Harald Schäfer [1, 2], will be discussed in more detail. As the name of this technique suggests, it is possible to transport solids from one place to another. This is achieved by utilizing a chemical equilibrium which has the solid to be transported and other gaseous reactants on one side, while only gaseous reactants are present on the other side. Since the temperature is used as the control variable, the equilibrium position must be temperature-dependent, i.e. ΔH ≠ 0. With a few exceptions, the latter is the rule anyway, so it is primarily important that the previously mentioned conditions for the states of aggregation are fulfilled. Furthermore, for some applications the direction of transport is important, i.e. whether the transport should be from "cold to hot" or "hot to cold". According to Schäfer, chemical transport can be divided into 3 steps [1]:

1. 1) Equilibration at _T1
2. 2) Transport of the equilibrium gas
3. 3) Equilibration at _T2

Equation <1> shows the general formulation of an equilibrium suitable for chemical transport.

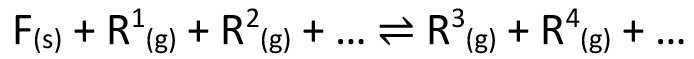
<1>

F = transported solid
R = gaseous reactants

According to Le Chatelier's principle, the direction of transport can be read from the sign of the reaction enthalpy. In the following, we take the simplified equilibrium according to equation <2> as a basis:

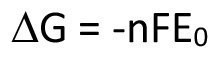
<2>

At ΔH > 0, a transport from hot to cold takes place and at ΔH < 0 a transport from cold to hot takes place. Figure 1 shows a schematic diagram of the chemical transport process.

Fig. 1: Schematic representation of the temperature-dependent equilibrium position during chemical transport

However, the transport velocity, which is proportional to the difference in the partial pressures of^R1 and^R2 in the temperature zones _T1 and _T2, depends on the exact value of ΔH and the value and sign of ΔS [3]. The rule is that there is no transport at ΔH = 0 and practically no transport at very high ΔH. In the case of an equilibrium as in equation <2>, in which the number of moles of the gas particles does not change, ΔS is naturally very small. For cases with larger ΔS, ΔH must also have the same sign. This is due to the fact that transport is suppressed by extreme equilibrium positions, i.e. with high ΔG. K must therefore not differ too much from 1.

According to equation <3>, the temperature dependence of chemical reactions results from the relationship between the Gibbs free enthalpy ΔG and the equilibrium constant K.

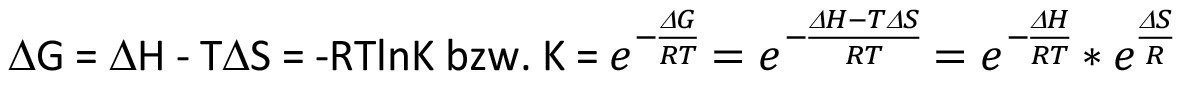
<3>

As is generally known, equilibrium 2 is on the side of the reactants if ΔG is positive and on the side of the products if ΔG is negative. Under these conditions, however, the absolute temperature T still remains as a parameter that influences the equilibrium position. With positive ΔG or ΔH, an increase in temperature leads to a greater K, i.e. the equilibrium is then less on the side of the reactants. With negative ΔG or ΔH, on the other hand, an increase in temperature leads to a smaller K, i.e. the equilibrium is then less strongly on the side of the products.

On a laboratory scale, a 2-zone temperature furnace is required to carry out chemical transport. The solid to be transported is melted into a glass ampoule, the ends of which are located in one or the other temperature zone. Ideally, only one reactant on the reactant side and one gaseous reactant on the product side are required. The easiest way to do this (the reactant side) is to melt it into the ampoule in a solid state together with the solid to be transported; the gaseous reactant on the product side is then formed automatically as part of the equilibration process. For this purpose, the lower end is cooled to the required temperature and the solid reactant is filled or condensed. Iodine is particularly suitable against this background if a corresponding usable equilibrium exists. If the ΔH is positive, the end of the glass ampoule with the reactants is positioned in the area with a higher temperature _T2; if the ΔH is negative, it is positioned in the area with a lower temperature _T1.

On the one hand, the closed reaction chamber creates the same total pressure in the entire ampoule. On the other hand, the different temperatures and the resulting temperature gradient lead to a location-dependent equilibrium position with the respective extremes in the areas of maximum and minimum temperature, i.e. at the ends of the ampoule. As a result, the partial pressures of the respective reactants at the site of dissolution or re-deposition differ for the same total pressure, whereby the resulting concentration gradient triggers diffusion processes. This leads to the corresponding net mass transfer. In addition, recrystallization processes also occur.

Here there is an analogy to the recrystallization of crystallites in contact with the mother liquor, an example of Ostwald ripening. This generally states that during the chemical or physical reformation of a phase, those species are formed initially and therefore only temporarily which are preferred due to the kinetics of the underlying processes. In the long term, however, thermodynamics prevail, which leads, for example, to recrystallization processes occurring after crystallization in contact with the mother liquor, in which the larger crystallites continue to grow at the expense of the smaller ones, while the latter dissolve. This is due to the fact that the mother liquor is undersaturated from the point of view of the smaller crystallites, but oversaturated from the point of view of the larger crystallites. Theoretically, this should result in only one large crystal(it) remaining at the end. However, this is usually not the case, as the proportion of the surface energy of the crystallites, the reduction of which is the driving force of Ostwald ripening, only makes a significant contribution to the total energy of the nuclei in comparatively small nuclei and crystallites.

The difference in crystallite sizes also plays a role in chemical transport for the same reason, but the driving force here is the fact that the underlying reaction is deflected out of equilibrium at all points in the existing temperature gradient. On the starting side of the reactants, the equilibrium is shifted to the product side, so that a net product formation takes place here, while on the transport target side the equilibrium is shifted to the reactant side, so that the reactants are formed here again on a net basis.

On a large scale, chemical transport is mainly used for the purification of metals. Well-known examples are the van Arkel de Boer process, which is used for the purification of titanium(eq. <4>), as well as the lunar process for the purification of nickel(eq. <5>).

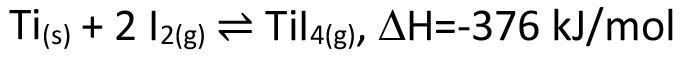
<4>

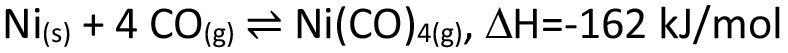
<5>

However, we most frequently encounter the principle of chemical transport in everyday life when using halogen lamps. These are based on the classic principle of the blackbody radiator, in which a heated solid emits a spectrum of electromagnetic waves depending on its temperature. In order to achieve the highest possible yield in the visible light range, very high temperatures are required at which the tungsten filament used tends to evaporate. If, in the course of this evaporation, areas with a slightly reduced filament diameter are formed, the resulting increased ohmic resistance leads to a further local temperature increase, so that the filament is bound to burn out at this point. By adding very small quantities of a halogen such as chlorine or iodine to the actual lamp gas krypton (which is used due to its poor thermal conductivity and therefore good insulating effect), a further, exactly opposite chemical transport process is superimposed on the evaporation process (transport from the hot tungsten filament to the comparatively cool inner wall of the lamp glass)(Eq. <6>), which brings tungsten from the cool lamp wall back to the hottest and therefore thinnest point of the tungsten filament. This allows temperatures of up to 3200 °C to be achieved, which is only around 200 °C below the melting point of tungsten. An extremely clever approach, patented by GE in 1959 [4]. However, this idea may also have arisen from the fact that the reverse case had previously been observed in atmospheres with traces of water, with increased erosion of the tungsten or molybdenum at thin points of a filament, due to equation <7> [5]. However, the knowledge that traces of iodine, for example, can significantly extend the service life of corresponding precursor lamps had already been known since 1918 [6].

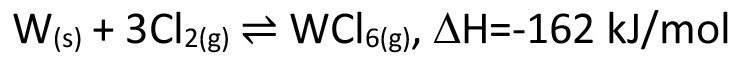
<6>

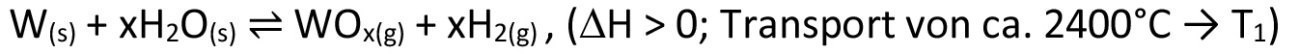
<7>

However, the most important process in macroeconomic terms is probably the blast furnace process for iron and steel production. Here, iron ore and coke serve as reactants. However, the carbon does not reduce the iron ore directly, but carbon monoxide is formed via the Boudouard equilibrium(Eq. <8>), which, as a gaseous reducing agent, can reduce the iron ore much faster and more completely than would be the case in a pure solid-state reaction.

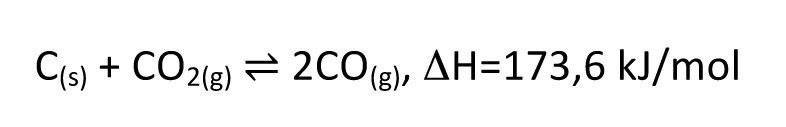
<8>

Incidentally, the advantage of gaseous reactants in surface technology is also used in the production of thermochemical coatings. Here, the foreign element is also offered "atom by atom" via gas phase equilibria, which could also be used for chemical transport. However, the driving force here is not a temperature gradient, but a concentration gradient of the foreign element in the substrate.

These relationships are reflected in Le Chatelier's aforementioned principle, also known as the principle of least constraint. According to this principle, a system avoids an externally imposed constraint by causing a shift in the system, which reduces the external constraint. Since the ampoule used for chemical transport is one and the same system, but is exposed to a forced temperature gradient, the shift becomes visible through a net solid transport.

At this point, the similarity to electrodeposition mentioned at the beginning becomes apparent. Here too, if we initially only consider the substrate to be coated, we change the electrochemical potential of the metal atom trunks ^Mez+, which correspond to the ions on the electrolyte side, by shifting the internal potential, i.e. the Galvani potential of the generally metallic substrate, see equation <9>.

<9>

The substrate/electrolyte phase boundary of such a so-called metal/metal ion electrode is semi-permeable, i.e. permeable, with regard to these metal atom trunks or metal ions, while the phase boundary for the other "component" of the metal, the electrons, is practically non-permeable with regard to the metal/metal ion electrode, as shown schematically in Figure 2.

The microscopic processes involved in the permeation reaction are deliberately omitted here, as is the fact that an electrode can very well release electrons into the electrolyte, e.g. to a redox couple such as ^Fe2+/Fe3+ or to the solvent, which in the case of water leads to the well-known hydrogen evolution as a side reaction.

The important relationship between classical and electrochemistry becomes clear when you consider the maximum work available in each case, which is expressed in Gibbs free enthalpy. Equation <10> shows the corresponding relationship with the equilibrium potential (open cell potential).

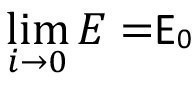
<10>

This can be understood to mean that as the current density approaches zero, the electrical work performed approaches a limit value, namely the Gibbs free enthalpy, which represents the maximum work that can be performed. At the same time, the overvoltages and also the IR drop (voltage dropping across the electrolyte) approach zero. This is expressed in equation <11>.

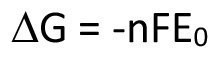
<11>

At first glance, the extraordinary thing about electrochemistry is precisely this possibility of being able to set electrochemical equilibrium positions, or more precisely half-cell positions, defined by a variable that can be easily controlled from the outside, such as the electrode potential (where E = difference of the electrode potentials). In this way, thermodynamically exact conditions can be specified that allow, for example, electrochemical reactions to be carried out with high selectivity. In most cases, the focus remains on one of the two electrodes, depending on whether the products are formed from the reactants by reduction or oxidation. If both the reductive and oxidative partial reactions are to be used profitably in order to increase efficiency, this is known as a 200% reaction. In classical chemistry, this is referred to as by-products, as opposed to waste products. An example of an industrially established 200% process is chlor-alkali electrolysis, in which hydrogen and sodium hydroxide are obtained as a by-product of chlorine production (actually a 300% process, as each electron converted is "utilized" three times). The advantage over classic reactions here lies in the natural local separation of the reaction spaces. In the case of chlorine production, this is even extremely important in order to prevent disproportionation of the chlorine in the alkaline.

In electroplating, the focus is normally on the cathode, although it is clear to every expert that the anode reaction deserves just as much attention in the interest of stable process conditions. In practice, in contrast to electrosynthesis, for example, galvanostatic processes are used here. This is mainly for practical reasons, as it allows constant deposition rates to be achieved, which simplifies the achievement of target specifications and time management during coating. In contrast to classical electrochemistry, we are also dealing, at least in electroforming, with a case in which the desired electrochemical reaction product remains on the substrate, the electrode, which actually serves as an aid. Even in electroforming, in which the deposited layer is separated from the substrate again in a second step, the presence of this substrate is absolutely essential, at least as an intermediary.

In the following, the parallels and differences between chemical transport and electrodeposition (electrochemical transport) will be shown:

From a thermodynamic point of view, a potential gradient is generated between the electrodes and the electrolyte during electrodeposition by sufficiently lowering the cathode potential or raising the anode potential, which causes the overall system to undergo equalization reactions that "aim" to bring the overall system back into equilibrium. Of course, the specialist has no interest in such an equalization; on the contrary, the cathodic deposition should continue unchanged while keeping the deposition parameters constant. This is ensured by taking suitable measures to ensure that the concentration ratios of the ions of the metal to be deposited in the electrolyte do not change on average. In the case of a soluble anode, the aim is therefore to achieve the same cathodic and anodic efficiency; in the case of an insoluble anode, continuous replenishment is required. Due to the generally high conductivity of the electrolyte, the potential gradient in the area of the electrode/electrolyte phase boundaries is very high, whereas it is comparatively low in the electrolyte, as only the ohmic electrolyte resistance has to be overcome there. The potential gradients at the phase boundaries, on the other hand, are the driving force of the electrochemical processes (breakdown reactions, see breakdown overvoltage) and also serve to compensate for concentration shifts in the electrolyte films (diffusion and reaction overvoltage) and the electrode surfaces (crystallization overvoltage) and the associated changes in ohmic resistance (resistance overvoltage). From the point of view of the cathode, the aim described above is to reduce the concentrations of metallic species in the electrolyte to such an extent that the cathodic and anodic partial reactions at the cathode take place at the same rate again, against the background of the desired equalization and thus a restoration of equilibrium states. Similarly, the anode "pursues" the goal of increasing the concentrations of the metallic species in the electrolyte to such an extent that the cathodic and anodic partial reactions at the anode take place at the same rate again. This is the first analogy to chemical transport, in which one and the same underlying chemical reaction strives for a locally variable state of equilibrium through a spatial temperature gradient. In electrodeposition using soluble anodes, there are two defined locations or planes (viewed perpendicular to the electrode surfaces) at or in which an equilibrium position corresponding to the respective electrode potential is sought through a net transfer of metal ions into the electrolyte (anode) or onto the electrode (cathode) when both electrodes are aligned plane-parallel. Now one could easily think of the Hull cell geometry in order to find an analogy to the spatial dependence of chemical transport. However, this analogy is only partial. In fact, a logarithmic progression of the primary current density occurs on the working electrode, caused by a variable distance to the counter electrode and thus a location-dependent ohmic electrolyte resistance. In contrast to chemical transport, in which the locally different equilibrium positions lead to the solid to be transported being transported to the respective extreme regions (here in relation to the temperature), with electrodes that are either cathodically or anodically polarized as a whole (or in equilibrium), there is no successive shift of the cathodically deposited metal to the areas with the highest field strength or primary current density. It is well known that the wide range of possibilities for influencing the scattering ability via the electrolyte composition means that even potential irregularities in the layer thickness due to inhomogeneities in the electric field can be prevented or mitigated. Electroplating therefore benefits from the fact that the interactions between the components in liquid electrolytes are significantly stronger than in a gas, which can be used profitably for the intended purpose. A similarity to chemical transport, on the other hand, can be seen when working with center conductors. These are located in the electric field between the actual electrodes and are therefore polarized in opposite directions at their ends, i.e. anodically or cathodically. This effect can therefore lead to simultaneous location-dependent material removal or deposition on the center conductor.

At this point, we must not forget that the previous considerations regarding chemical transport only referred to the thermodynamic equilibrium position, even though it has already been noted that transport is generally diffusion-controlled. For electrodeposition, the usual approach to deposition kinetics (transport of ions in the electrolyte and on the electrode surfaces, upstream and downstream reactions, leakage reaction) has already been discussed. Can we therefore speak of differently balanced equilibria in an analogy to chemical transport?

One major difference is, of course, that the spatial separation of oxidation and reduction typical of electrochemistry means that only half-cells are considered locally, whereas chemical transport involves "fully-fledged" reaction equations. If you look at the overall reaction in electrodeposition with a soluble anode, it is relatively sobering, as according to equation <12> it does not actually appear to be a chemical reaction in the narrower sense.

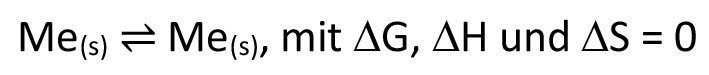
<12>

In this example, nothing is chemically converted at all, but merely transported due to the spatial separation of anode and cathode. Since all atoms of an isotopically pure element are absolutely identical or we always assume the same isotope distribution, we can actually speak of a transport, even if the majority of the deposited metal does not originate at the anode but in the electrolyte. Of course, the structure of the deposited metal can also differ in its crystallite size and other substances co-deposited by secondary reactions, which depends largely on the selected parameters and plays a very important role in electroplating practice. We can see that, although no energy is stored chemically, the transport still "costs" something because, depending on the speed, we have to apply a certain voltage which, multiplied by the total amount of charge that has flowed (the integral of the cell current), reflects the required energy input. According to the first law of thermodynamics, however, this energy is not destroyed, but has merely changed its form and contributed as thermal energy to heating up the system or the environment. The fact that we can actually speak of an (electro)chemical process here is also shown by the fact that we would have to work under more drastic conditions if we only used physical processes, for example by changing the state of aggregation (transport via the liquid or gaseous state). The electrochemistry here is therefore based on the two combined half-cells, which are identical in our example, just as chemical transport is always based on the same reaction. Both half-cells are deflected in opposite directions, as the oxidation must take place in one and the reduction in the other. This effort does not cancel each other out, but adds up, see equation <13>.

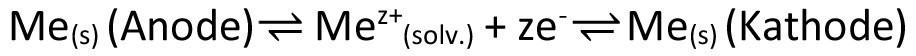
<13>

The electrons are not in the electrolyte with the metal cations, but "wander" in the outer circuit. Figure 2 shows the schematic process.

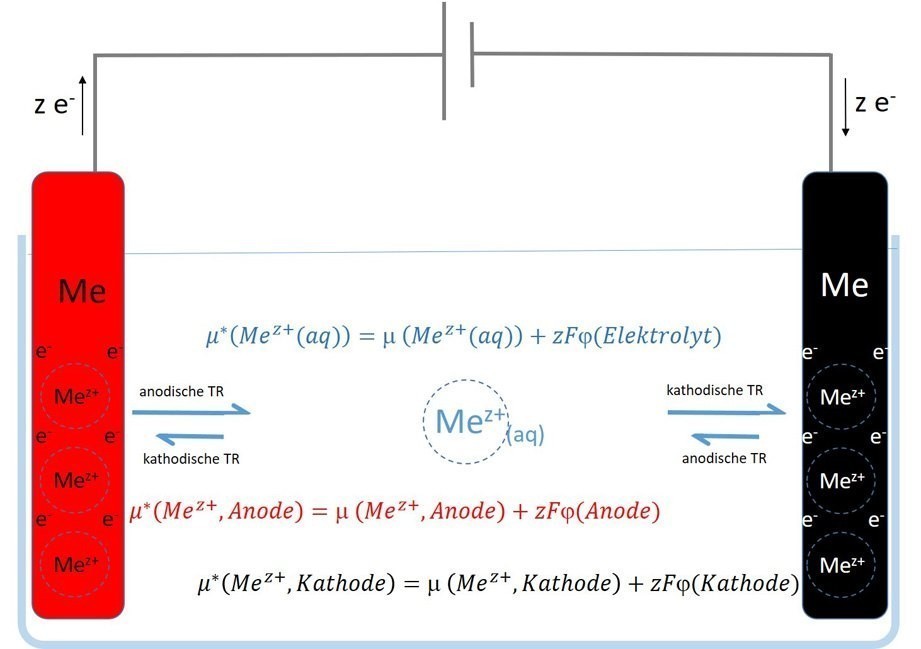Fig. 2: Schematic diagram of electrodeposition with soluble anode and half-cell equilibria that occur

If we compare the two processes of chemical and electrochemical transport, heterogeneous reactions occur in both cases at the starting and end points, with a transport process taking place in between in the gas or electrolyte, or in the external circuit. In both cases, the absolute amount of transported substance is proportional to the available surface area (in the case of chemical transport, for example, if it is a correspondingly heated filament), as long as there is no limitation. For higher rates, the question of the rate-determining step automatically arises. As in the electrolyte, a concentration gradient also forms in the gas phase, whereby the diffusion rate decreases with increasing total pressure. At high pressures (and smaller mean gas molecule distances), (thermal) convection must be taken into account as a further transport process, comparable to that in the electrolyte. Here, too, limitations occur due to the diffusion process itself if the available deposition surface is sufficiently large.

In addition to temperature and electrical voltage, pressure is also a possible parameter. The Haber-Bosch process can serve as an example here, where the yield of ammonia in the synthesis of hydrogen and nitrogen is increased in the continuous process using the Le Chatelier principle.

Table 1 summarizes the similarities and differences between chemical and electrochemical transport. For the sake of completeness, a comparison is also made with processes that work with pressure gradients.

To summarize, a comparison of chemical and electrochemical transport reveals sufficient similarities (but also revealing differences) to justify such a designation for electrodeposition. However, it is not a question of compulsively trying to find new names for familiar things, but rather of looking at the electrodeposition process from a different, unusual perspective, which, I hope, will enrich the process at one point or another and inspire new ideas and approaches.

Literature

[1] H. Schäfer; H. Jacob; K. Etzel: Z. Anorg. Allg. Chem., 286, 1956, 27
[2] H. Schäfer: Chemische Transportreaktionen, Verlag Chemie GmbH, Weinheim, 1962
[3] H. Schäfer; H, Jacob; K. Etzel: Z. Anorg. Allg. Chem., 286, 1956, 42
[4] US patent 2883571
[5] C.J. Smithells: Tungsten, Chapman and Hall, London, 3rd ed., 1952
[6] US Patent 1267888