In den Jahren 2017 und 2018 wurde die DIN 50957 „Prüfung galvanischer Bäder Galvanisierungsprüfung mit der Hull-Zelle“ vom DIN-Ausschuss NA 062-01-61 AA routinemäßig überprüft und die Norm in zwei Teile geteilt.
Der Teil 1 (DIN 50957-1:2016-02, Teil 1: „Standard-Hull- Zelle“) beruht auf der DIN 50957-1978 und beschreibt die Standard-Hull-Zelle. Der Teil 2 (DIN 50957-2:2019, Teil 2: „Spezielle Prüfzellen“) beinhaltet eine gegenüber der Standardzelle verlängerte Version der Hull-Zelle (Lang-Zelle) sowie zusätzlich gewinkelte Kathodenbleche. Mit den in den Normen vorgegebenen Geometrien wurden 2D- und 3D- Simulationen zur primären und sekundären Stromdichteverteilung mit dem Finite-Elemente-Programmen COMSOL Multiphysics (electrochemical modul) sowie Cell Design durchgeführt.
Zusätzlich wurden die Simulationen mit experimentellen Werten verglichen.
1 Einleitung
In der 2019 erarbeiteten DIN 20957-2 [1] wurden neben einer Langversion der Hull-Zelle die Maße von Winkel- elektroden für eine galvanotechnische Beschichtung festgelegt. In einem ersten Teil [2] wurde neben der Standard- Hull-Zelle die Lang-Zelle beschrieben und für diese COMSOL®-Simulationen [3] mit der finiten-Elemente- Methode (FEM) Stromdichte-Verteilungen erstellt und mit experimentellen Ergebnissen verglichen. Dabei wurden die Simulationen in 2D durchgeführt, da kein Mehrwert von 3D-Simulationen bei deutlich höherem Rechenaufwand zu erwarten war sowie idealisierte Bedingungen angenommen (Elektroden liegen an Wänden an, einfache Elektrodenreaktionen).
Hier werden noch einige ergänzende Überlegungen vorgestellt, um die Simulationsmodelle von 2D zu 3D zu erweitern, was schließlich zu den Winkelkathoden führt. Diese haben eine ähnliche Geometrie und die Abscheidung kann im Unterschied zur Standard-Hull-Zelle unter Bewegung mit erzwungener Konvektion durchgeführt werden. Daneben ergeben sich weitere Unterschiede: Änderung der Geometrie hinsichtlich Winkel und Dimension, verringerte Länge der schrägen Flanke, fehlende isolierende Wände direkt an der Kathode zur Vergleichsmäßigung der Feldverteilung über die Elektrolyttiefe.
Da diese veränderten (Rand-)Bedingungen Simulationen in 3D erfordern, wurde zuerst durch 2D-Simulationen geprüft, welchen Einfluss eine Dimensionsverringerung, verkleinerte Elektroden und Zellen sowie segmentierte Elektroden auf die Stromdichteverteilung haben. Des Weiteren wurde eine mehrfache Kerbstruktur mit weiter verkleinerten Vertiefungen der Kathode mit einbezogen.
Die 3D-Simulationen wurden an der Standard-Hull-Zelle begonnen, deren Bodenplatte sowie die isolierenden Begrenzungen nacheinander entfernt wurden, was schließlich zur Simulation der Stromdichte-Verteilung der Winkelelektroden führt. Bezüglich des Modells der sekundären Stromdichte-Verteilung wurden im Wesentlichen die in [2] angegebenen kinetischen Parameter wiederverwendet (Tab. 1), in Ausnahmefällen werden die geänderten Parameter jeweils angegeben.
2 Simulation der Hull-Zellen mit verkleinerten und segmentierten Elektroden sowie verkleinerten Zellen
Die Winkelkathoden sind nach [1] freistehend und haben etwas kleinere Abmessungen im Vergleich zur Standard-Hull-Zelle, die Länge des schrägen Bereichs beträgt maximal noch 25 mm. Daher erscheint es interessant, Simulationen der Hull-Zelle in dieser Richtung weiter zu führen und die Geometrie entsprechend zu öffnen.
|
Parameter |
|||
|
Elektrolytleitfähigkeit |
κ |
0,1 |
S/cm |
|
Austauschstromdichte |
j0 |
10-8 |
A/cm2 |
|
Kathodischer Tafelfaktor |
bK |
39,0 |
V-1 |
In Teil 1 [2] wurden entsprechend der Norm die Hull- Zellen mit perfekt an den Seitenwänden abschließenden Elektroden in 2D simuliert. Dabei ergab sich, dass der Anoden-Kathoden-Abstand aufgrund der homogenen Feldverteilung bis zur schrägen Wand keinen Einfluss auf die Stromdichteverteilung hat, was der Erwartungshaltung vieler Praktiker widerspricht. Daher wurden Simulationen für die sekundäre Stromdichteverteilung durchgeführt, bei denen die Elektroden in ihrer Breite um dc verkleinert wurden (< 10 cm), wobei die Grundgeometrie der Standard-Hull-Zelle (Außenmaße, Elektrodenhöhe) unverändert blieb, so dass zwischen den Elektroden und den Wänden b und d bei den Punkten 3 und 4 (vgl. Abb. 1 in [2]) ein isolierender Bereich (Spalt, dc/2) entsteht. Weiterhin wurde eine Vergrößerung des Anoden-Kathoden-Abstands mit einbezogen, wobei die daraus folgende Verlängerung der Hull-Zelle gegenüber den Standard-Maßen mit dy angegeben wird.
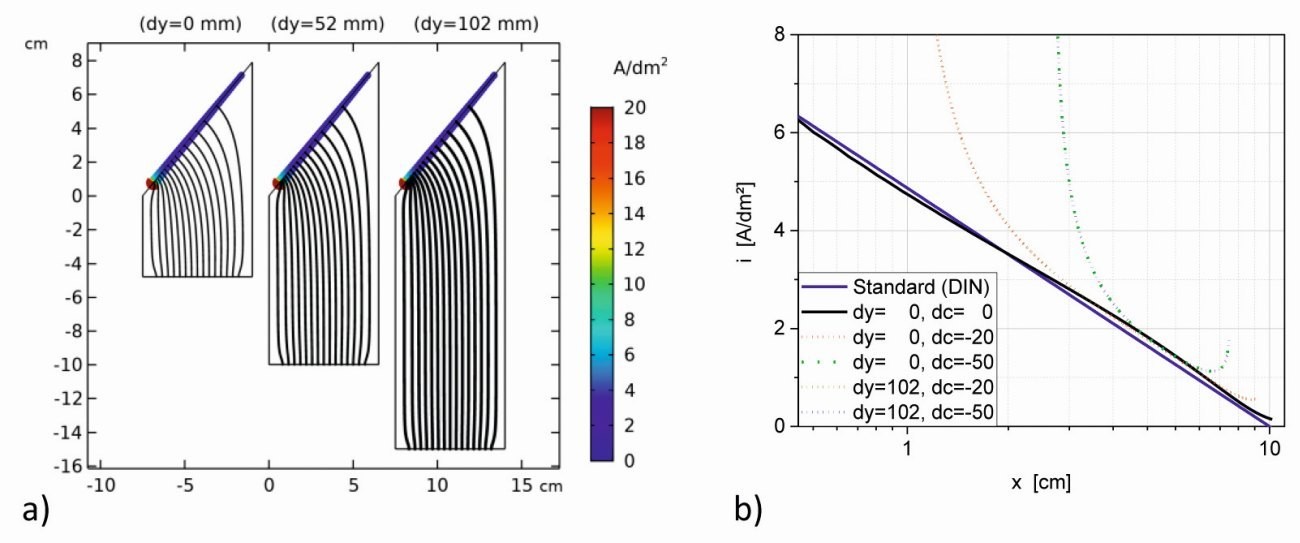 Abb. 1: a) Simulierte Feldverteilungen von Standard- (dy=0 mm) und verlängerten Hull-Zellen (dy=52 mm und dy=102 mm) mit beidseitig um je 2,5 cm verkürzten Kathoden (dc=-50 mm) (I=0,5 A) und b) Vergleich der Stromdichteverteilungen der verlängerten Zellen mit verkürzten Elektroden (dc=-20 mm bzw. -50 mm und I=0,8 bzw. 0,5 A)) mit der Standard-Hull- Zelle (dc=0, I = 1 A)
Abb. 1: a) Simulierte Feldverteilungen von Standard- (dy=0 mm) und verlängerten Hull-Zellen (dy=52 mm und dy=102 mm) mit beidseitig um je 2,5 cm verkürzten Kathoden (dc=-50 mm) (I=0,5 A) und b) Vergleich der Stromdichteverteilungen der verlängerten Zellen mit verkürzten Elektroden (dc=-20 mm bzw. -50 mm und I=0,8 bzw. 0,5 A)) mit der Standard-Hull- Zelle (dc=0, I = 1 A)
2.1 Verkleinerte Elektroden
Bei verkleinerten Elektroden, sowohl Kathode als auch Anode, bleibt die homogene (sekundäre) Feldverteilung in der Mitte der Zelle weitgehend erhalten, siehe Abbildung 1a. Wiederum zeigt sich, dass das elektrische Feld den zur Verfügung stehenden Raum vollständig ausnutzt und die isolierenden Bereiche mit für die Feldverteilung zuständig sind. Obwohl nun eine deutliche Erhöhung der Stromdichte an den seitlichen Elektrodenkanten (Hundeknocheneffekt) auftritt, bleiben die Stromdichteverteilungen im mittleren Bereich auf der Seite c von 4–7 cm (1,5–4,5 cm bezogen auf die verkleinerte Elektrode) ähnlich und nähern sich dort Gleichung <2> aus [2] an (Abb. 1b). Der Kathoden-Anoden-Abstand bestimmt somit primär die nötige Zellspannung, trägt aber nicht zu einer gleichmäßigeren Stromdichteverteilung bei.
2.2 Segmentierte Kathoden
Im Unterschied zu den in Abschnitt 2.1 gezeigten schmaleren Elektroden wird von Kudryavtsev, Nachinov und Mitarbeitern [4] eine segmentierte Hull-Zelle mit z. B. 10 einzelnen Elektrodenstreifen zur Bestimmung der Makro- streufähigkeit beschrieben. Dazu nutzten sie das Verhältnis der Schichtdicken bzw. der Massenzunahme bestimmter Streifen. Prinzipiell lassen sich so mit entsprechenden Messanordnungen die einzelnen Ströme der Segmente messen. Praktische Anwendungen segmentierter Elektroden betreffen die klassische Gestellgalvanik oder die dort auch verwendeten Hilfskathoden. Auch außerhalb der Metallabscheidung sind segmentierte Elektroden hinsichtlich der Stromdichteverteilung von Interesse: für homogene Redoxsysteme z. B. Hexacyanoferrate [5] und z. B. gasentwickelnde Elektroden.
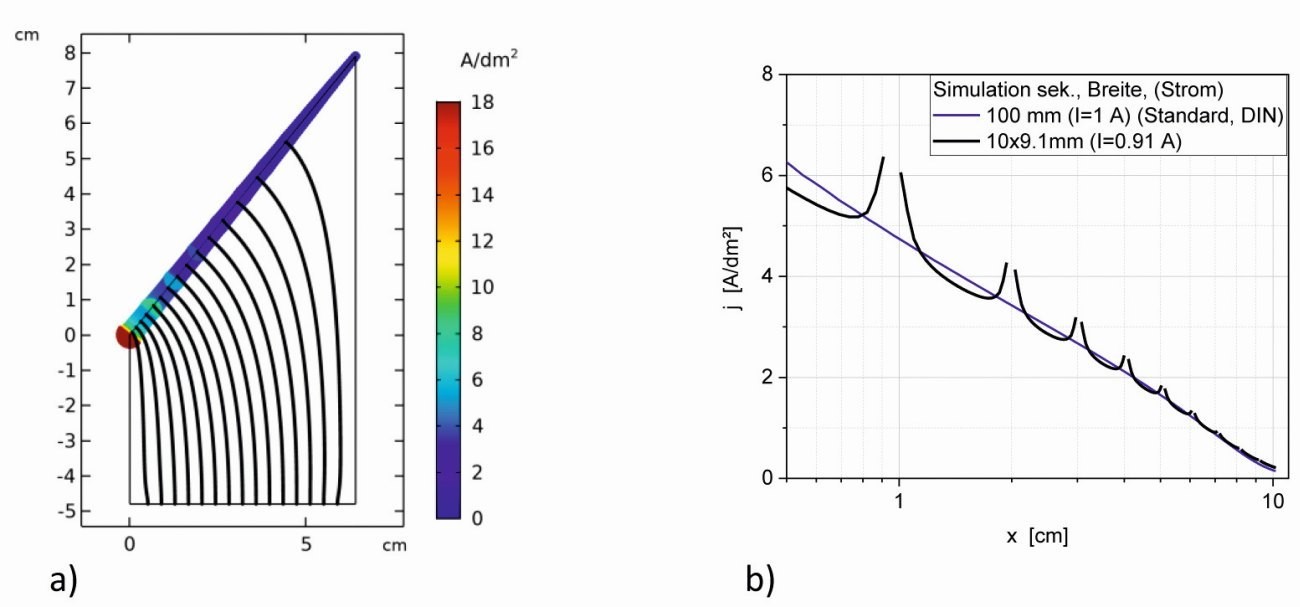 Abb. 2: Sekundäre Strom- dichteverteilungen einer segmentierten Hull-Zelle (Kathode: 10 Segmente à 9,1 mm, 1 mm Abstand, verkleinerte Anode: 57,6 mm breit (adäquat zu der Breite aller Kathoden- streifen), I = 0,91 A, a) Stromlinien im Elektrolyten, b) Stromdichten in Abhängigkeit von x im Vergleich mit der Standard- Hull-Zelle
Abb. 2: Sekundäre Strom- dichteverteilungen einer segmentierten Hull-Zelle (Kathode: 10 Segmente à 9,1 mm, 1 mm Abstand, verkleinerte Anode: 57,6 mm breit (adäquat zu der Breite aller Kathoden- streifen), I = 0,91 A, a) Stromlinien im Elektrolyten, b) Stromdichten in Abhängigkeit von x im Vergleich mit der Standard- Hull-Zelle
Abbildung 2 zeigt die Simulationsergebnisse einer solchen Segmentation in 10 Segmente à 9,1 mm Breite und einem Abstand von 1 mm. Da sich die Kathodenfläche dabei um ca. 9 % verringert, wurden zur Vergleichbarkeit auch die Anode und der angelegte Strom entsprechend reduziert.
Die Stromlinien weisen global denselben Verlauf wie bei der nicht segmentierten Variante (Abb. 2a). Dabei wird aber der Feldverlauf an den Segmenten in diesem Maßstab nicht aufgelöst. Deutlich sichtbar ist die Stromdichteerhöhung an den Kanten der einzelnen Segmente, sowie das Absinken der Stromdichten auf der Fläche – besonders im hohen Stromdichtebereich (Abb. 2b). Sieht man von den erhöhten Stromdichten an den Rändern der Streifen ab, folgt die gemittelte Kurve dem Verlauf der unsegmentierten Zelle. Im niedrigen Stromdichtebereich unter 1 A/dm2 kommt es zur direkten Annäherung an die Kurve der sekundären Stromdichteverteilung und die Randüberhöhungen verschwinden nahezu.
 Abb. 3: Querschliffe (horizontal) mit Schichtdickenmessungen des 10 mm breiten Mittelstreifens einer Dreistreifenanordnung, 1 mm Abstand zu 2 benachbarten Streifen; a) Randbereich und b) mittlerer Bereich
Abb. 3: Querschliffe (horizontal) mit Schichtdickenmessungen des 10 mm breiten Mittelstreifens einer Dreistreifenanordnung, 1 mm Abstand zu 2 benachbarten Streifen; a) Randbereich und b) mittlerer Bereich
Ähnliche Stromdichteerhöhungen an Kanten wurden mit einer Dreistreifenanordnung experimentell nachgewiesen [6]. In Abbildung 3 sind Schichtdickenmessungen am Rand (Abb. 3a) und in der Mitte (Abb. 3b) eines 10 mm breiten mit Nickel beschichteten Streifens aus einer Dreistreifenanordnung dargestellt, der im Abstand von 1 mm zu zwei benachbarten Streifen positioniert war. Der Schichtdickenunterschied beträgt hier zwischen Mitte (ca. 20 µm) und Rand (ca. 23–24 µm) bis zu 20 % während die Simulation bis zu ca. 30 % vorhersagt.
2.3 Verkleinerung der Standard-Hull-Zelle
Neben der insbesondere für die alkalische Zinkabscheidung eingesetzten Lang-Zelle [1] werden für spezielle Elektrolyte auch verkleinerte Hull-Zellen verwendet. Vom Fachgebiet Elektrochemie und Galvanotechnik wird neben Eigenbau-Zellen dazu die Tenori-Zelle von der Firma Yamamoto [7] für Elektrolyte auf Basis ionischer Flüssigkeiten eingesetzt. In Tabelle 2 sind die Maße dieser Zelle im Vergleich zur Standard-Hull-Zelle angegeben. Während die Kathodenlänge um die Hälfte verringert ist, ist die Kathodenfläche um den Faktor 3 verkleinert. Der für die Stromdichteverteilung wichtige spitze Winkel ist dagegen nur geringfügig kleiner.
|
Dimensionen / mm |
V / ml |
<) (cd) / ° |
|||||
|
a (Anode) |
b |
c* (Kathode) |
d |
h (Füllhöhe) |
|||
|
Tenori |
30 |
20 |
51 (50) |
60 |
30 |
36 |
36,9 |
|
DIN (Standard) |
64 |
48 |
102 (100) |
127 |
44 |
250 |
39.0 |
Da die Simulation der Tenori-Zelle keine wesentlichen Unterschiede zur Standard-Hull-Zelle zeigte, wurde die Standard-Hull-Zelle in jeder Dimension um den Faktor 10 verkleinert, um einen möglichen Geometrieeinfluss deutlicher erkennbar zu machen. Da dabei die Kathodenfläche um den Faktor 100 verkleinert wurde, wurde auch der Strom von 1 A auf 0,01 A verringert, um die mittlere Stromdichte jm beizubehalten und damit die Vergleichbarkeit zu gewährleisten. Trotz der Verringerung der Zellgröße bleibt man immer noch im Maßstab der Makro- streufähigkeit.
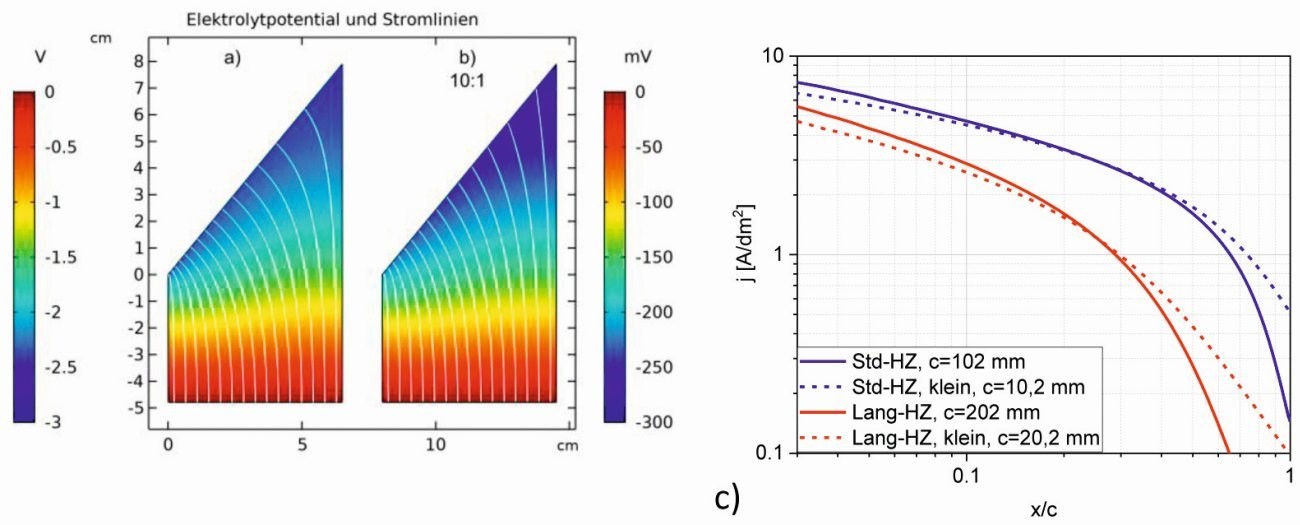 Abb. 4: Feldverteilung und Stromlinien der a) Standard-Hull- Zelle (1 A) und b) der um 100 verkleinerten Zelle (10 mA), c) Stromdichte- Verlauf der Stan- dard-Hull-Zelle, Lang-Zelle sowie der jeweils verkleinerten Zellen
Abb. 4: Feldverteilung und Stromlinien der a) Standard-Hull- Zelle (1 A) und b) der um 100 verkleinerten Zelle (10 mA), c) Stromdichte- Verlauf der Stan- dard-Hull-Zelle, Lang-Zelle sowie der jeweils verkleinerten Zellen
Schon in den Diagrammen zur Potentialverteilung und den Stromlinien (Abb. 4a und b, Potential an der Anode rot, an der Kathode blau) zeigen sich deutliche Unterschiede, die in erster Näherung auf den kürzeren Elektrodenabstand zurückzuführen sind. Aber auch an der Krümmung der Stromlinien sieht man, dass die Stromdichteverteilung der verkleinerten Zelle gleichmäßiger ist. Trägt man die Stromdichte gegenüber der relativen Länge auf, wird das durch den flacheren Verlauf der Stromdichte bestätigt (Abb. 4c). Einen größeren Effekt zeigt die Simulation für die sekundäre Stromdichte-Verteilung der verkleinerten Lang-Zelle, insbesondere im Bereich x/c > 0,5 kommt es nicht zu dem entsprechenden Stromdichteabfall wie bei der standardisierten Lang-Zelle.
Als Schlussfolgerung verbleibt, dass bei ähnlichen Zellen bei einer starken Verkleinerung die sekundäre Stromdichte-Verteilung etwas gleichmäßiger wird und die Unterschiede in den Stromdichten nicht so gravierend ausfallen.
3 Zweidimensionale Simulation der sekundären Stromdichte-Verteilung von gewinkelten Strukturen
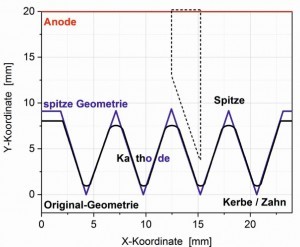 Abb. 5: Mikroformstruktur: Original- und spitze Geometrie (Cell Design) sowie skizzierte Hull-Zelle-Struktur Neben der Geometrie der Hull-Zelle treten in der Praxis ähnliche trapezförmige Strukturen auf, die sich mit einer zweidimensionalen Simulation beschreiben lassen. Dabei kann einerseits das Ziel darin bestehen, eine möglichst gleichmäßige Schichtdickenverteilung zu erzielen, aber auch darin, keilförmige Strukturen zu schaffen.
Abb. 5: Mikroformstruktur: Original- und spitze Geometrie (Cell Design) sowie skizzierte Hull-Zelle-Struktur Neben der Geometrie der Hull-Zelle treten in der Praxis ähnliche trapezförmige Strukturen auf, die sich mit einer zweidimensionalen Simulation beschreiben lassen. Dabei kann einerseits das Ziel darin bestehen, eine möglichst gleichmäßige Schichtdickenverteilung zu erzielen, aber auch darin, keilförmige Strukturen zu schaffen.
Ein solcher Fall sind die in Abbildung 5 abgebildeten Graben- oder Kerbstrukturen, die im Vergleich zur Standard-Hull-Zelle wesentlich kleiner sind. Zusätzlich ist die trapezförmige Struktur eingezeichnet. Die schrägen Flanken betragen ca. 8 bis 10 mm, die Kerbtiefe ca. 6–9 mm und der Kathoden-Anoden-Abstand einige cm, so dass auch hier noch der Maßstab der Makrostreufähigkeit zutreffend ist. In Vorbereitung auf die nur dreidimensional zu simulierenden Winkelkathoden wurden diese Kerbstrukturen zweidimensional mit Cell Design [8] berechnet. Dabei lag der Schwerpunkt auf der abgerundeten Grabenstruktur entsprechend Abbildung 5.
Der halbe Winkel beträgt hier 16,4°, und ist noch etwas kleiner im Vergleich zur Lang-Zelle. Die Elektrodenlänge der Kathode verkürzt sich von der spitzen zur abgerundeten Form von 78 auf 65 mm. Durch die seitlich begrenzenden Wände wie bei der Hull-Zelle ist das elektrische Feld vor der Anode homogen. Die Stromdichteverteilung verhält sich, wie in Kapitel 2.3 beschrieben, im Wesentlichen analog zur Hull-Zelle.
3.1 Simulation der primären und sekundären Stromdichte-Verteilung
Die Simulation wurde für den Fall der sekundären Stromdichte-Verteilung mit etwas veränderten Parametern für einen Sulfamat-Nickel-Elektrolyten durchgeführt (j0 = 10-8 A/cm2; α = 0,75 bK= 39 V-1; T = 50 °C; κ = 0,1 S/cm). Als mittlere Stromdichte jm wurde ein Wert von 0,45 A/dm2 ausgewählt.
In Abbildung 6a ist der Verlauf der sekundären Stromdichte über die Breite der Struktur dargestellt. Deutlich erkennt man, dass bei der spitzen Struktur an den Spitzen höhere Stromdichten und in den Kerben (Zahn) niedrigere gegenüber der abgerundeten Struktur anliegen, aber in beiden Fällen gibt es eine signifikante Stromdichte in den Kerben. Dabei ist der Stromdichte-Verlauf jeweils an den 3 Spitzen bzw. 4 Kerben gleich. Vergleicht man die Stromdichteverteilung der Kerbstruktur mit der der Lang-Zelle (ähnlicher Winkel) bei gleicher mittlerer Stromdichte, jm z.B. von 1 A/dm2, sind die Stromdichten in der Mikrostruktur mit 2,4 zu 0,4 A/dm2 bzw. in der Lang-Zelle mit > 5 bis 0,02 A/dm2 (Pkt. 3 und 4 in Abb. 1 in [2]) in der Spitze größer und in der Kerbe kleiner. Dass ist darauf zurückzuführen, dass sowohl die Spitzen als auch die Zähne entsprechend abgerundet sind. Dementsprechend wird bereits seit längerem schon für die Design-Phase von Bauteilen auf eine entsprechende Kantenglättung hingewiesen [9].
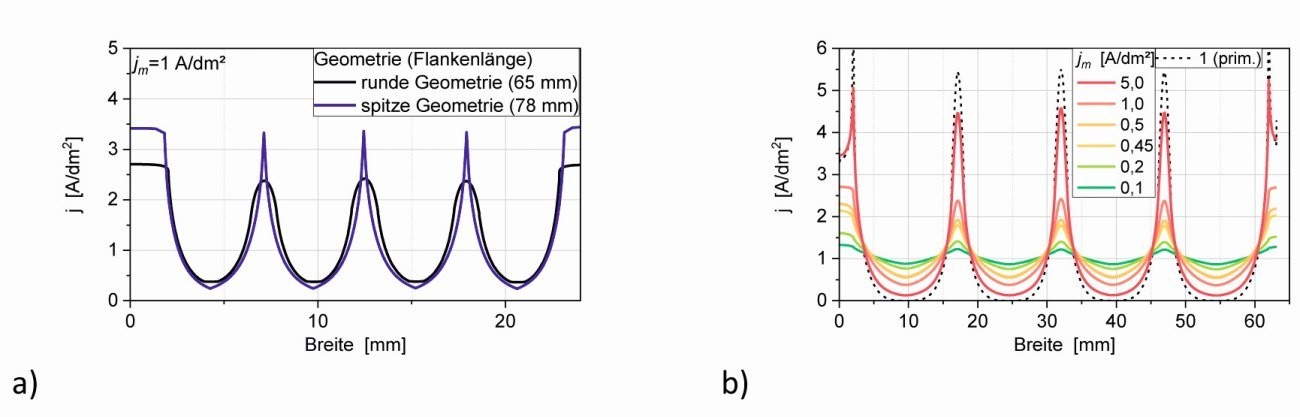 Abb. 6: a) Sekundäre Stromdichteverteilung vs. Breite der Kathode b) Abhängigkeit der relativen sekundären Stromdichteverteilung j/jm vs. Elektrodenlänge (die Elektrodenlänge der 24 mm breiten Struktur beträgt ca. 64 mm)
Abb. 6: a) Sekundäre Stromdichteverteilung vs. Breite der Kathode b) Abhängigkeit der relativen sekundären Stromdichteverteilung j/jm vs. Elektrodenlänge (die Elektrodenlänge der 24 mm breiten Struktur beträgt ca. 64 mm)
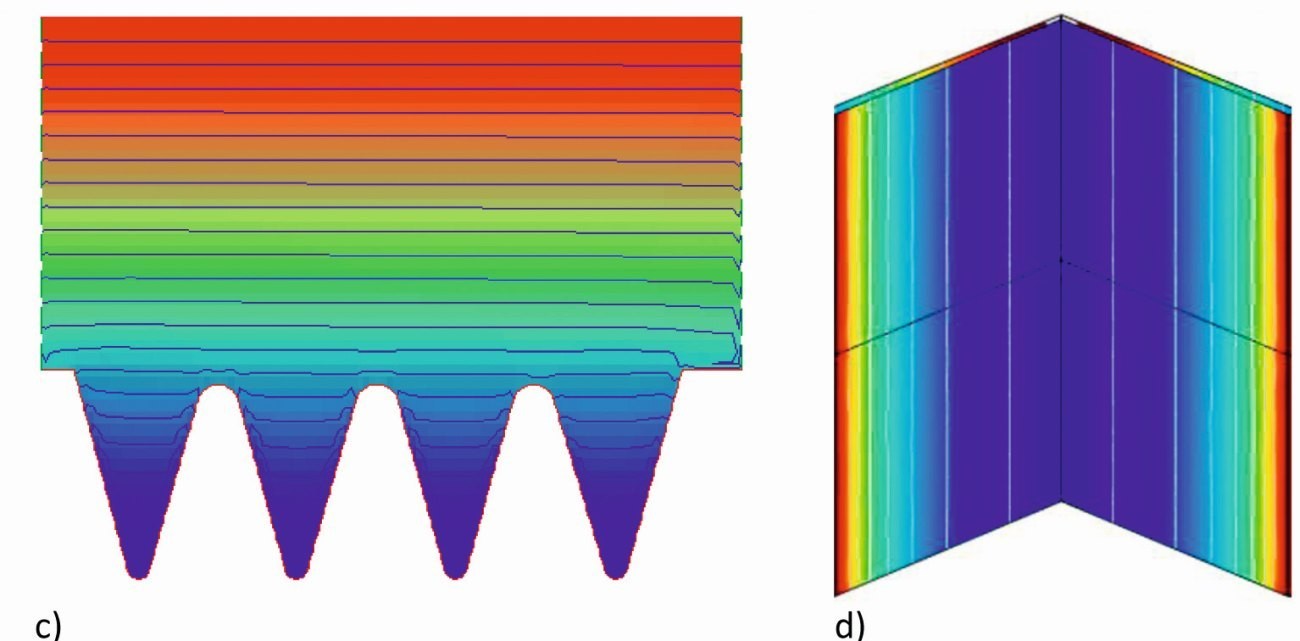 Abb. 6: c) Potential-Verteilung d) Stromdichte-Verteilung über die Tiefe einer Kerbe (3D, von oben)
Abb. 6: c) Potential-Verteilung d) Stromdichte-Verteilung über die Tiefe einer Kerbe (3D, von oben)
Mit der abgerundeten Grabenstruktur wurde weiterhin die primäre Stromdichte-Verteilung sowie die Stromdichte-Abhängigkeit der sekundären berechnet (Abb. 6b, Stromdichte vs. Elektrodenlänge). Die Simulation der primären Stromdichte-Verteilung (gestrichelte Kurve) zeigt, dass in der Kerbe die Stromdichte im Unterschied zur Simulation der sekundären auf 0 absinkt, also in diesem Fall die Spitzen komplett die Tiefen abschirmen.
Die Simulation der sekundären Stromdichte-Verteilung zeigt, dass die Äquipotentiallinien in die Kerbstruktur eintreten (Abb. 6c) und dadurch die Stromdichte in den Gräben nicht so stark abnimmt im Vergleich zur primären Feldverteilung. So ist dort auch zu erwarten, dass sich eine merkliche Abscheidung und die gewünschte Zahnstruktur ausbildet. Über die Tiefe der Kerbstruktur ergibt sich aufgrund der seitlichen Wände eine konstante Stromdichte (Abb. 6d, hier in 3D berechnet).
Um zu prüfen, welche Stromdichte für eine ausreichende Schichtdicke im Kerbgrund am günstigsten ist, wurde in der Simulation die mittlere Stromdichte jm variiert. In Abbildung 6b ist die Stromdichteverteilung für die verschiedenen Stromdichten dargestellt. Deutlich erkennt man, dass das Verhältnis der Stromdichten der Spitze und des Kerbgrunds mit abnehmender Stromdichte jm kleiner und damit günstiger wird. In [2] wurde schon darauf hingewiesen, dass die Stromdichte-Potential-Kurve mit kleinerer Stromdichte flacher wird und damit der Polarisationsfaktor P ansteigt. Der Verlauf der Stromdichte auf der schrägen Flanke kann analog zur Standard-Hull-Zelle mit Gleichung <1> approximiert werden.
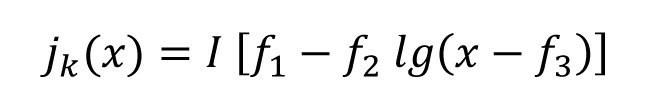 Gl. <1>
Gl. <1>
3.2 Experimentelle Ergebnisse – Galvanoformung
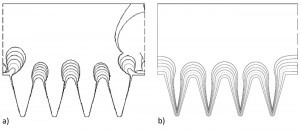 Abb. 7: Simulation Mikroformstruktur; a) primäre Schichtdickenverteilung 6-mal je 50 h (jm=0,15 A/dm2) und b) sekundäre Schichtdickenverteilung 6-mal je 40 h 0,45 A/dm2Im Unterschied zu den bisherigen Simulationen in Kapitel 3.1 werden hier größere Schichtdicken abgeschieden, so dass sich die Ausgangsgeometrie mit der Zeit ändern wird und damit auch die Stromdichten. Sowohl mit Cell Design als auch mit COMSOL lassen sich mit der Methode „Moving boundary“ die zeitlichen Geometrieänderungen gut simulieren. Im Prinzip wird iterativ vom Zeitpunkt t die Stromdichteverteilung und daraus die zum Zeitpunkt t+Δt resultierende Schichtdickenverteilung berechnet.
Abb. 7: Simulation Mikroformstruktur; a) primäre Schichtdickenverteilung 6-mal je 50 h (jm=0,15 A/dm2) und b) sekundäre Schichtdickenverteilung 6-mal je 40 h 0,45 A/dm2Im Unterschied zu den bisherigen Simulationen in Kapitel 3.1 werden hier größere Schichtdicken abgeschieden, so dass sich die Ausgangsgeometrie mit der Zeit ändern wird und damit auch die Stromdichten. Sowohl mit Cell Design als auch mit COMSOL lassen sich mit der Methode „Moving boundary“ die zeitlichen Geometrieänderungen gut simulieren. Im Prinzip wird iterativ vom Zeitpunkt t die Stromdichteverteilung und daraus die zum Zeitpunkt t+Δt resultierende Schichtdickenverteilung berechnet.
Zunächst wurde die primäre Schichtdicken-Verteilung berechnet, siehe Abbildung 7a. Es zeigt sich das gleiche Bild analog zur Stromdichte-Verteilung, dass die Abscheidung nur auf die Spitzen konzentriert ist, wodurch sich zylinderförmige Wülste („Köpfe“) ausbilden. Die Kerben werden von den Spitzen abgeschirmt, so dass keine Auffüllung erfolgt, was jedoch das eigentliche Ziel der Abscheidung ist. Zusätzlich erkennt man auch bei der Simulation ein unkontrolliertes Wachstum der Nickelschicht, was sich in der Praxis als Ausbildung großer Knollen zeigt. Hier ist das auf eine unkorrekte Ausbildung der Oberflächenstruktur während der sukzessiven Simulation nach einer längeren Zeit zurückzuführen.
Die Simulation der sekundären Schichtdicken-Verteilung lässt ein besseres Ergebnis erwarten (Abb. 7b), da die Stromdichte in den Gräben nicht so stark im Vergleich zur Simulation der primären Feldverteilung abnimmt, so dass dort auch eine merkliche Abscheidung erfolgt und sich die gewünschte Zahnstruktur ausbildet. Ganz verhindern lässt sich anscheinend aber das stärkere Schichtdickenwachstum an den Spitzen nicht, so dass im Kerbgrund die Schichtdicken immer niedriger bleiben. Prinzipiell kann es dazu führen, dass die Schichten auf den Spitzen zusammenwachsen und ein Hohlraum entsteht.
Abbildung 8 zeigt eine von der Firma Kapp Niles zur Verfügung gestellte vernickelte Kerbstruktur, die in einem Nickel-Sulfamat-Elektrolyten gefertigt wurde. In Abbildung 8a und b ist der Querschliff dieser Probe im Ausgangszustand und beschichtet dargestellt [10]. Die Form der Abscheidung in den Gräben stimmt gut mit der durch Simulation erhaltenen sekundären Stromdichteverteilung (Abb. 8b) überein, wobei die im Experiment erhaltene Schichtdicke an der Spitze ca. das Vierfache von der in der Kerbe beträgt. Sobald aus der Rundung im Kerbgrund ein spitzer Winkel geworden ist, treffen die Schichten von beiden Seiten aufeinander, und man kann den bekannten Effekt der Kantenschwäche beobachten, siehe Abbildung 8c und d.
 Abb. 8: Nickel- Abscheidung aus Sulfamat-Elektrolyten: Vergleich zwischen Experiment und Simulation a) Ausgangsstruktur, b) Querschliff
Abb. 8: Nickel- Abscheidung aus Sulfamat-Elektrolyten: Vergleich zwischen Experiment und Simulation a) Ausgangsstruktur, b) Querschliff
 Abb. 8: c) Kerbe aus c), d) Simulation der Schichtdicken der Kerbe, Ausschnitt aus Abbildung 7b
Abb. 8: c) Kerbe aus c), d) Simulation der Schichtdicken der Kerbe, Ausschnitt aus Abbildung 7b
Als Schlussfolgerung kann man aus diesen experimentellen Ergebnissen ziehen, dass die Simulation mit der sekundären Stromdichte-Verteilung die Praxis schon gut abbilden kann.
Schaut man sich nicht nur das Schichtdickenwachstum sondern auch die Stromdichten zu den unterschiedlichen Zeiten an, zeigt sich, dass die Elektrodenlänge und -fläche zunimmt (Abb. 7) und damit sukzessive die mittlere Stromdichte jm kleiner wird. In Abbildung 9 ist die Stromdichte-Verteilung nach 40 h und 240 h einmal über die konstante Breite (Abb. 9a) und das andere Mal über die effektive Elektrodenlänge (Abb. 9b) dargestellt. Dadurch wird deutlich, dass mit der Geometrieänderung die Stromdichteverteilung mit zunehmender Zeit ungleichmäßiger wird. Insbesondere nimmt die Stromdichte am Kerbgrund (Zahn) sowie auch an den schrägen Kanten ab, während sie an den Spitzen und am Rand größer wird.
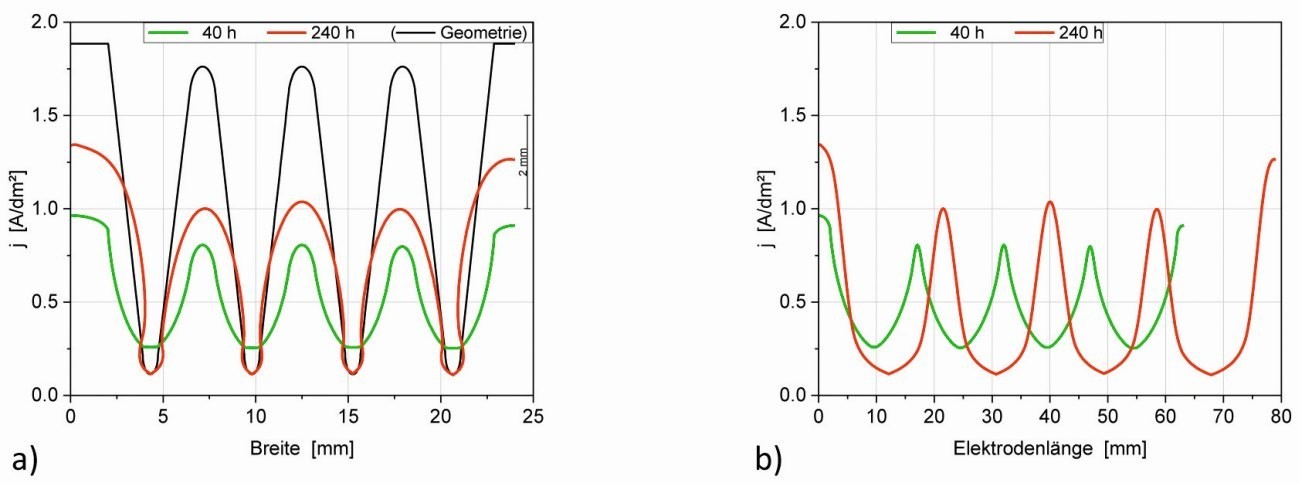 Abb. 9: Stromdichteverteilung in der Mikrostruktur nach verschiedenen Zeiten: a) entlang der Strukturbreite (X-Koordinate) und b) entlang der (sich ändernden) Elektrodenlänge
Abb. 9: Stromdichteverteilung in der Mikrostruktur nach verschiedenen Zeiten: a) entlang der Strukturbreite (X-Koordinate) und b) entlang der (sich ändernden) Elektrodenlänge
3.3 Simulationen zur Verbesserung der Schichtdickenverteilung
Da gerade für die Galvanoformung die experimentellen Aufwendungen sehr hoch sind, lohnen sich hier Simulationen, die in wesentlich kürzeren Zeiten zu Empfehlungen für die Praxis kommen. Zur Verbesserung der Schichtdickenverteilung wurden weitere Simulationen zur sekundären Stromdichteverteilung mit geringeren Stromdichten durchgeführt (siehe auch oben Abb. 6b für t = 0).
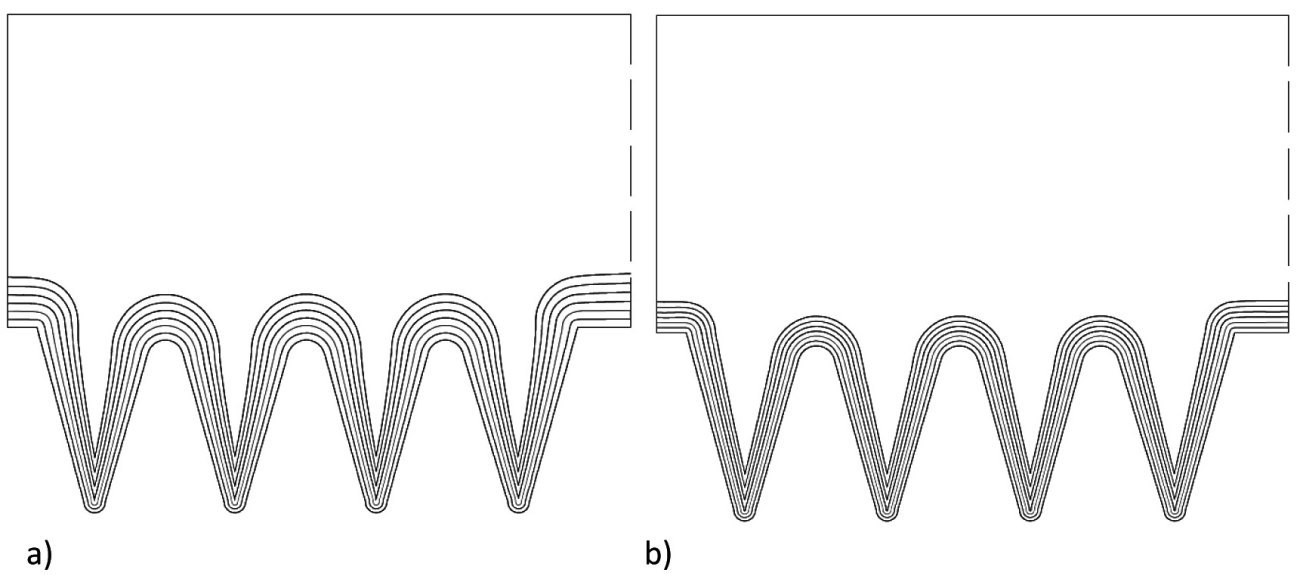 Abb. 10: Variation der Stromdichte zur Verbesserung der Schichtdickenverteilung a) 0,2 A/dm2 480 h je 80 h und b) 0,1 A/dm2, 720 h je 120 h
Abb. 10: Variation der Stromdichte zur Verbesserung der Schichtdickenverteilung a) 0,2 A/dm2 480 h je 80 h und b) 0,1 A/dm2, 720 h je 120 h
Abbildung 10 zeigt die entsprechenden Ergebnisse, wobei es mit der Abnahme der angelegten Stromdichte von 0,45 (vgl. Abb. 7b) über 0,2 zu 0,1 A/dm2 zu einer deutlichen Verbesserung kommt.
Dies geht so weit, dass mit einer starken Verringerung der mittleren Stromdichte nahezu dieselbe Stromdichte in den Kerben wie auf den Spitzen erzielt werden kann. Da dabei jedoch der Zeitaufwand deutlich steigt, muss man zwischen der Stromdichte und der Beschichtungszeit abwägen und ein individuelles Optimum finden, dass sich z. B. an der zu erreichenden Schichtdicke im Kerbgrund orientiert. Auch eine Änderung der mittleren Stromdichte über verschiedene Zeitintervalle der Abscheidung ist möglich.
– wird fortgesetzt –
Literatur
[1] DIN50957-1 und -2
[2] Schmidt, U.; Peipmann, R.; Bund, A.: Galvanotechnik 112(3), 2021, 301
[3] COMSOL Multiphysics®, COMSOL AB, Tegnergatan 23, SE-111 40 Stockholm
[4] Kudryavtsev, N.T.; Kuznetsov, V.P.; Nachinov, G.N.; Pachushkina, L.A.: Zhurnal Prikladnoi Khimii 54(3), 1981, 580 und Nachinov, G.N. und Kudryavtsev, N. T.: Itogi Nauki Tekh., Ser. Elektrokhimiya, 15 (1979), 179
[5] Chmielowiec, B.; Cai, T.; Allanore, A.: Journal of The Electrochemical Society 163(5), 2016, E142–E146
[6] Strauß, T.; Sun, Y.; Schmidt, U.: Galvanotechnik 105 (2014) 264
[7] Firmenschrift (Katalog) von Yamamoto-MS Co., LTD, Tokyo, Japan
[8] CELL-DESIGN®, Software for Computer Aided Design and Simulation of Electrochemical Cells, L-Chem, Inc., 13909 Larchmere Blvd. Shaker Heights, OH 4412
[9] Galvanogerechtes Konstruieren und Fertigen industrieller Bauteile, ZVO-Broschüre 97030, 2012
[10] Schorn, S.; Fritz, M.; Schmidt, U.; Bund, A.: Experiment und Simulation bei der Galvanoformung mit Nickel- Elektrolyten, Vortrag ZVO-Tagung Garmisch-Partenkirchen 2016
[11] Salloum, B.; Gruia, V.; Schmidt, U.; Bund, A.: unpubliziert 2018


