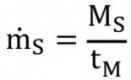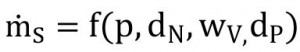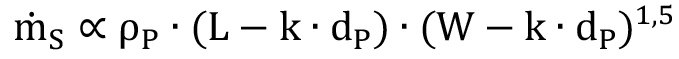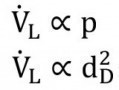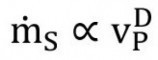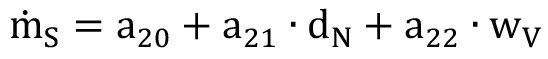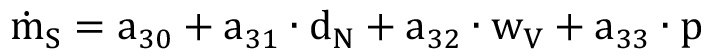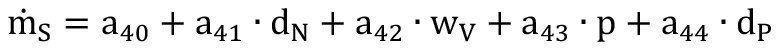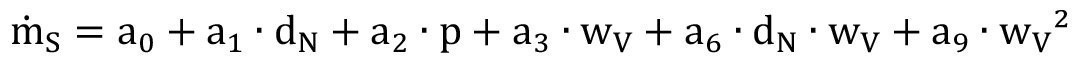Twitter
Facebook
Linkedin
1 Einführung
Der Strahlmitteldurchsatz gehört zu den wichtigsten Kennwerten des Strahlens mit festen Strahlmitteln [12, 13], und die Optimierung dieses Prozessparameters trägt wesentlich zur Erhöhung der Effektivität von Strahlprozessen bei. Aus Untersuchungen zum Einsatz des Strahlens mit festen Strahlmitteln zum Entschichten [6–8, 13, 17] und zur fertigungstechnischen Materialbearbeitung [11, 12] ist bekannt, dass optimale Werte für den Strahlmitteldurchsatz existieren. In Abbildung 1 sind zwei Beispiele für den Abtrag von organischen Korrosionsschutzbeschichtungen von einem Stahlsubstrat dargestellt. In beiden Fällen existiert ein optimaler Wert für den Strahlmitteldurchsatz, bei dem die jeweils höchste Flächenleistung erreicht wird: 25 kg/min für das metallische Strahlmittel, und 17 kg/min für das mineralische Strahlmittel. Der Strahlmitteldurchsatz in einem Druckluftsystem hängt von einer Reihe von Prozess- und Werkstoffkennwerten ab, insbesondere von statischem Luftdruck, Düsendurchmesser, Strahlmittelgröße und -dichte und Dosierventilkonfiguration [1, 2, 10, 17]. Das Ziel der im Beitrag beschriebenen Untersuchungen bestand in der Bewertung relevanter Einflusskennwerte sowie in der Modellierung des Dosierprozesses auf der Basis statistischer Untersuchungen.
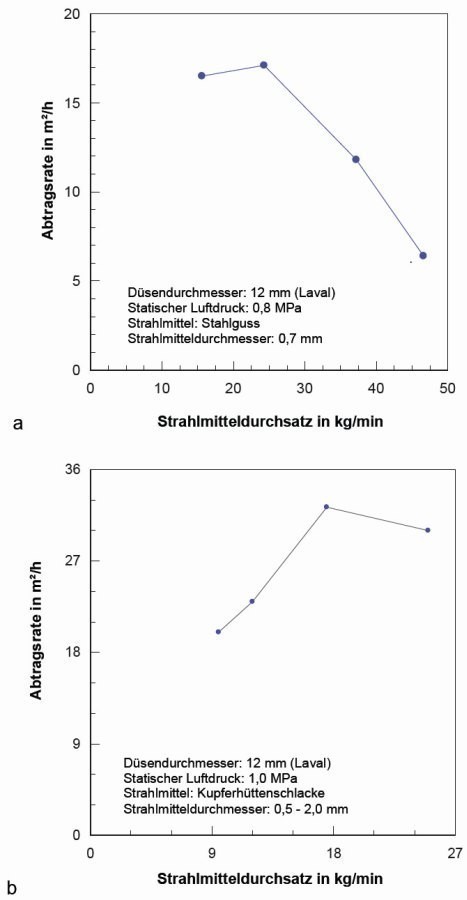Abb. 1: Zusammenhang zwischen Abtrags- rate und Strahlmitteldurchsatz. Beschichtung: 2 Schichten Epoxid (2 x 180 µm), Stahlsubstratunter- grundvorbereitung: Sa 2½ (siehe Momber, 2008). Es ergeben sich Maximalwerte der Abtragsrate bei einem Strahlmittel- durchsatz von 25 kg/min (Stahlguss) bzw. 18 kg/min (Kupferhütten- schlacke)
2 Versuchsaufbau
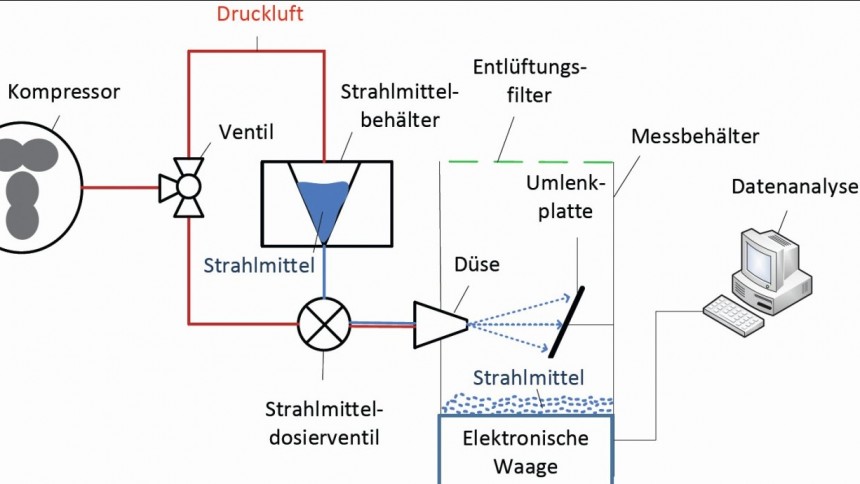
Der Versuchsaufbau ist in Abbildung 2 dargestellt. Der Strahlmittelbehälter war vom Typ „Taifun 8000“; er war mit einem pneumatisch gesteuerten Strahlmitteldosierventil „ADV 80“ausgestattet. Das völlig geöffnete Ventil wurde als Ventilöffnungsgrad „100 %“ definiert, während das völlig geschlossene Ventil als Ventilöffnungsgrad „0 %“ definiert wurde. Der Strahlmitteldurchsatz wurde als Quotient von Strahlmittelmasse und Messdauer bestimmt:
Gl. <1>
In der Gleichung ist ṁs der Strahlmitteldurchsatz in kg/min, MS ist die gemessene Strahlmittelmasse in kg, und tM ist die Messdauer in Minuten. Die Strahlmittelmasse wurde mit einer elektronischen Waage mit einer Genauigkeit von ±100g gemessen. Die Messdauer betrug eine Minute pro Messung, wobei pro Parameterkombination drei Messungen durchgeführt wurden. Die folgenden Prozess- und Werkstoffkennwerte wurden variiert: Dosierventilöffnungsgrad, statischer Luftdruck, Düsendurchmesser und Strahlmittelkorngröße. Die Einstellwerte/Faktoren sind in Tabelle 1 gelistet. Die Kennwerte für das verwendete nichtmetallische Strahlmittel (Kupferhüttenschlacke) finden sich in Tabelle 2 ,und die Kennwerte für das verwendete metallische Strahlmittel (Stahlguss) finden sich in Tabelle 3.
|
Faktor |
Einheit |
Stufe |
Stufe |
|
1) Gemessen am Strahlmittelbehältereinlass; 2) Divergent-konvergent (Laval) |
|||
|
Statischer Luftdruck1) |
MPa |
0,6; 0,8; 1,0 |
0,6; 0,8; 1,0 |
|
Düsenduchmesser2) |
mm |
8; 10; 12 |
8; 10; 12 |
|
Ventilöffnungsgrad |
% |
40; 50; 75; 100 |
30; 40; 50; 75; 100 |
|
Strahlmitteldurchmesser |
mm | 2,6 |
0,4; 0,6 |
|
Kennwerte |
Einheit |
Bereich |
|
1) Gemäß ISO 11124-4 |
||
|
Typ |
– |
Kupferhüttenschlacke1) |
|
Korngröße |
mm |
0,5 bis 2,0 |
|
Kornform |
– | kantig |
|
Werkstoffdichte |
kg/m3 |
3.700 |
|
Schüttdichte |
kg/m3 |
1.850 |
|
Härte |
Mohs |
> 7 |
|
Kennwert |
Einheit |
Bereich |
|
1) Gemäß ISO 11124-3; 2) Laut Datenblatt des Herstellers |
||
|
Typ |
– |
Stahlguss mit hohem Kohlenstoffgehalt1) |
|
Zusammensetzung |
% |
C≥0,85; Si≥0,8; 0,6≤Mn≤1,2; S≤0,05; P≤0,05 |
|
Korngrößenbereiche2) |
mm |
Fein: 0,35 bis 1,18 > 1,00 mm (5 %) > 0,60 mm (55 %) > 0,35 mm (100 %) |
|
mm |
Grob: 0,18 bis 0,85 > 0,71 mm (5 %) > 0,60 mm (20 %) > 0,42 mm (50 %) > 0,30 mm (70 %) > 0,18 mm (100 %) |
|
|
Kornform |
– |
kantig |
|
Werkstoffdichte |
kg/m3 |
7.600 |
|
Schüttdichte |
kg/m3 |
4.500 |
| Härte | HRc | 65,2 |
3 Statistische Untersuchungen
Die folgende Beziehung wurde den statistischen Untersuchungen zugrunde gelegt:
Gl. <2>
Hier sind p (statischer Luftdruck), dN (Düsendurchmesser), wV (Ventilöffnungsgrad) und dP (Strahlmitteldurchmesser) die Faktoren, und ṁs (Strahlmitteldurchsatz) ist der Zielkennwert. Ein vollfaktorieller Versuchsplan wurde erstellt [19]. Zunächst wurden die residualen Kennwerte ermittelt, um den zufälligen Charakter der Versuchsabläufe zu prüfen. Schließlich wurden die Ergebnisse mittels ANOVA (Analysis of Variance) bewertet, um den Einfluss jedes Faktors und von Faktorkombinationen auf die Versuchsergebnisse (Zielkennwert) zu ermitteln. Die Analysen basierten auf einem Signifikanzlevel P = 0.05 (Confidence Level 95 %). Der Einfluss eines Faktors oder einer Faktorenkombination ist somit insignifikant für P > 0.05 [5]. Die folgenden Kennwerte wurden für die jeweiligen Faktoren/Faktorkombinationen bestimmt: Freiheitsgrad, Fehlerquadratsumme, mittlerer statistischer Fehler, F-Wert und P-Wert [5]. Anschließend wurden die Beziehungen mittels Regressionsanalysen modelliert [16].
4 Ergebnisse
4.1 Ergebnisse der Strahlmitteldurchsatzmessungen
Die Ergebnisse der Messungen für beide Strahlmittelsorten ergaben, dass sich der Strahlmitteldurchsatz erhöhte, wenn die Werte für statischen Luftdruck, Düsendurchmesser, Ventilöffnungsgrad stiegen und wenn der Wert für die Strahlmittelkorngröße (Stahlguss) sank. Die Ergebnisse stimmten qualitativ mit Ergebnissen anderer Autoren überein [4, 10, 20].
Für den Massendurchsatz vergleichsweise grober Partikel (weniger als 3 % kleiner als 250 µm), die durch einen rechteckigen Querschnitt gefördert werden, kann die folgende Gleichung angewendet werden [3, 18]:
Gl. <3>
In der Gleichung ist ρP die Strahlmittelschüttdichte, L ist die Länge der Dosieröffnung, W ist die Breite der Dosieröffnung, dP ist die Strahlmittelgröße und k=2,4 ist ein Strahlmittelbeiwert für kantiges Strahlmittel [18]. Die Faktoren statischer Luftdruck und Düsendurchmesser sind in Gleichung <3> nicht enthalten. Eine Erweiterung kann folgendermaßen vorgenommen werden (mit W=vW):
Gl. <4>
|
Exponent |
Metallisches Strahlmittel |
Nichtmetallisches Strahlmittel |
| A | 1.0 | 1.0 |
| B | 2.0 | 1.52 |
| C | 1.2 | 1.48 |
Die Exponenten A, B und C sind in Tabelle 4 gelistet. Der lineare Verlauf zwischen statischem Luftdruck und Strahlmitteldurchsatz (A=1.0) bestätigt Ergebnisse [10] für nichtmetallisches Strahlmittel (Korund) und [14] für metallisches Strahlmittel (Stahlshot). Während der Exponent A vom Strahlmitteltyp unabhängig war, wurden die Exponenten B und C vom Strahlmitteltyp bestimmt. Wenn in einer Druckluftstrahlanlage Werte für statischen Luftdruck oder Düsendurchmesser steigen, erhöht sich der durchgesetzte Luftstrom nach den folgenden Gesetzen [13]:
Gl. <5>
In den Gleichungen ist 
der Luftvolumenstrom. Da nach dem Kontinuitätsgesetz der Luftvolumenstrom in einem System bei vorgegebenem statischen Luftdruck die Luftgeschwindigkeit determiniert [13], und die Luftgeschwindigkeit wiederum die Fördergeschwindigkeit für Strahlmittel bestimmt, kann ein genereller Zusammenhang der folgenden Form prognostiziert werden:
Gl. <6>
In der Gleichung ist vP die Strahlmittelgeschwindigkeit im Druckluftsystem. Ein entsprechender Zusammenhang wird in [15] berichtet, die einen Exponent D = 1.2 ermittelten.
Der Einfluss der Schüttdichte auf den Strahlmitteldurchsatz in Gleichung <4> wurde durch einen Vergleich der Ergebnisse der beiden Strahlmittelsorten zumindest qualitativ bestätigt. Der Einsatz des wesentlich schwereren Stahlgusses bewirkte eine deutliche Zunahme des Strahlmitteldurchsatzes. Die Korngrößen beider Strahlmittelsorten waren allerdings nicht identisch.
4.2 Ergebnisse der statistischen Untersuchungen
4.2.1 Residual-Analyse
Der zufällige Charakter der Messergebnisse wurde für beide Strahlmittelsorten auf der Grundlage der Residual- Analysen bestätigt. Die Strahlmitteldurchsätze waren normal verteilt, es wurden keine Ausreißer erzeugt (Residual versus Fit), und die Ergebnisse folgten keinem zeitlichen Trend (Residual versus Order). Systematische Fehler konnten daher für beide Strahlmittelsorten ausgeschlossen werden, und es konnten statistische Methoden zur Bewertung der Ergebnisse benutzt werden.
4.2.2 Metallisches Strahlmittel
Die ANOVA-Ergebnisse für das metallische Strahlmittel sind in Tabelle 5 wiedergegeben. Sie zeigten, dass Ventilöffnungsgrad und Düsendurchmesser statistisch extrem signifikante Einflüsse (P < 0.001) auf den Strahlmitteldurchsatz ausübten, während die Einflüsse von statischem Luftdruck und Strahlmittelkorngröße statistisch insignifikant waren. Signifikante Interaktionen zwischen den Faktoren konnten für keine der Faktoren nachgewiesen werden.
|
Quelle |
Freiheitsgrade |
Sum of squares |
Mean square |
F-Test |
P-Wert1) |
|
1) P > 0,05 insignifikant; P < 0,01 sehr signifikant; P < 0,001 extrem signifikant [5] |
|||||
|
Modell |
17 |
10.343,4 |
608,4 | 34,70 |
0,000 |
|
Linear |
|||||
|
Düsendurchmesser |
2 |
2.467,10 |
556,90 | 31,70 |
0,000 |
|
Luftdruck |
2 | 427,80 | 52,60 | 3,00 | 0,061 |
|
Ventilöffnung |
4 |
7.187,50 |
1.545,4 |
88,10 |
0,000 |
|
Korngröße |
1 | 36,00 | 34,30 | 1,95 | 0,0169 |
|
2-Way Interactions |
|||||
|
Düsendurchmesser*Luftdruck |
4 | 126,00 | 30,40 | 1,74 | 0,160 |
|
Düsendurchmesser*Korngröße |
2 | 94,10 | 47,60 | 2,71 | 0,078 |
|
Luftdruck*Korngröße |
2 | 4,90 | 2,50 | 0,14 | 0,869 |
|
Fehler |
42 | 736,80 | 17,50 | ||
|
Gesamt |
59 | 11.080,20 | |||
4.2.3 Nichtmetallisches Strahlmittel
Die ANOVA-Ergebnisse für das nichtmetallische Strahlmittel sind in Tabelle 6 wiedergegeben. Sie zeigten, dass nur der Ventilöffnungsgrad einen statistisch signifikanten Einfluss hatte (P < 0.05). Bezüglich der Faktoreninteraktionen wies die lineare Kombination von „dD*vW“ einen sehr signifikanten Zusammenhang (P < 0.01) auf. Bei der quadratischen Kombination bestand ein extrem signifikanter statistischer Zusammenhang für die Kombination „vW*vW“ (P < 0.001).
|
Quelle |
Freiheitsgrade |
Sum of squares |
Mean square |
F-Test |
P-Wert1) |
|
1) P > 0,05 insignifikant; P < 0,01 sehr signifikant; P < 0,001 extrem signifikant [5] |
|||||
|
Modell |
9 | 1.118,20 | 124,20 | 42,36 | 0,000 |
|
Linear |
|||||
|
Düsendurchmesser |
1 | 0,02 | 0,018 | 0,01 | 0,939 |
|
Luftdruck |
1 | 0,24 | 0,243 | 0,08 | 0,776 |
|
Ventilöffnung |
1 | 16,24 | 261,70 | 84,10 | 0,028 |
|
2-Way Interactions |
|||||
|
Düsendurchmesser*Luftdruck |
1 | 3,35 | 3,35 | 1,14 | 0,297 |
|
Düsendurchmesser* |
1 | 27,13 | 27,13 | 9,25 | 0,006 |
|
Luftdruck*Ventilöffnung |
1 | 0,94 | 0,94 | 0,32 | 0,577 |
|
Quadratisch |
|||||
|
Düsendurchmesser* |
1 | 0,47 | 0,47 | 0,16 | 0,693 |
|
Luftdruck*Luftdruck |
1 | 0,05 | 0,05 | 0,02 | 0,901 |
|
Ventilöffnung*Ventilöffnung |
1 | 45,76 | 45,76 | 15,6 | 0,001 |
|
Fehler |
22 | 64,53 | 2,933 | ||
|
Gesamt |
31 | 1.182,80 | |||
4.3 Regressionsgleichungen
4.3.1 Metallisches Strahlmittel
Die Ergebnisse wurden mittels Regressionsgleichungen weiter aufbereitet. Die Ergebnisse für das metallische Strahlmittel wurden mit drei linearen Regressionsgleichungen analysiert; im Detail:
2-Parameter-Regression:
Gl. <7>
3-Parameter-Regression:
Gl. <8>
4-Parameter-Regression:
Gl. <9>
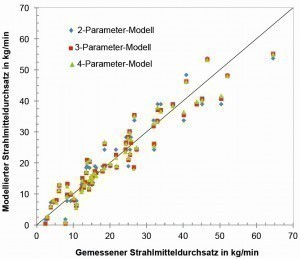Abb. 3: Korrelation zwischen mittels Regressionsmodellen ermittelten und gemessenen Strahlmitteldurchsätzen für das metallische Strahlmittel (Stahlguss)
Die Regressionsparameter aij finden sich in Tabelle 7. Eine weitere Verfeinerung der Regressionen erfolgte mittels zweier Methoden, und zwar „Mallows‘-CP“ und „PRESS“ (predicted residual error sum of squares) [16]. Die Ergebnisse der Berechnungen in Tabelle 8 und Abbildung 3 zeigten, dass eine 3-Parameter-Regression ohne Berücksichtigung der Strahlmittelkorngröße hinreichend genaue Werte lieferte. Ergebnisse der Regressionsrechnungen sind in Abbildung 3 gegen die gemessenen Werte für den Strahlmitteldurchsatz aufgetragen.
|
Koeffizient |
Wert |
SE-C1) |
t-Wert |
P-Wert2) |
VIF3) |
|
2-Parameter-Regression |
|||||
|
a20 |
-37,20 |
3,76 |
-9,90 |
0,000 |
– |
|
a21 |
0,59 |
0,031 |
19,24 |
0,000 |
1,03 |
|
a22 |
2,66 |
0,36 |
7,37 |
0,000 |
1,03 |
|
3-Parameter-Regression |
|||||
|
a30 |
-43,40 |
4,33 |
-10,04 |
0,000 |
– |
|
a31 |
2,63 |
0,34 |
7,63 |
0,000 |
1,04 |
|
a32 |
0,58 |
0,029 |
29,77 |
0,000 |
1,05 |
|
a33 |
8,97 |
3,47 |
2,58 |
0,012 |
1,02 |
|
4-Parameter-Regression |
|||||
|
a40 |
-39,50 |
5,40 |
-7,33 |
0,000 |
– |
|
a41 |
2,59 |
0,34 |
7,49 |
0,000 |
1,05 |
|
a42 |
0,59 |
0,031 |
19,18 |
0,000 |
1,17 |
|
a43 |
9,10 |
3,46 |
2,63 |
0,011 |
1,02 |
|
a44 |
-6,99 |
5,83 |
-1,20 |
0,236 |
1,12 |
|
1) Standardabweichung in % |
|||||
|
Modell |
Bewertungskennwert |
||||
|
R2 |
R2Adj |
PRESS |
Mallows’-Cp |
S1) |
|
|
2-Parameter |
89,6 | 89,3 | 1.317 | 9,2 | 4,5 |
|
3-Parameter |
90,7 | 90,2 | 1.215 | 4,4 | 4,3 |
|
4-Parameter |
91,0 | 90,3 | 1.227 | 5,0 | 4,2 |
4.3.2 Nichtmetallisches Strahlmittel
Die Ergebnisse wurden mittels einer quadratischen Regressionsgleichung (Gl. <10>) weiter aufbereitet.
Gl. <10>
Gl. <11>
Obgleich die Standardabweichung (1,7 %) einen geringen und der Regressionskoeffizient (RAdj2 = 0.92) einen befriedigenden Wert aufwiesen, zeigten die hohen Werte für VIF (42 bis 344), dass die Regression einen hohen Grad an Multikolinearität aufwies. Ein kritischer oberer Wert für VIF ist 10 [9]. Multikolinearität kann u.a. signifikante Faktoren überdecken und zu Änderungen im Vorzeichen von Regressionskonstanten führen. Eine Standardisierung der Variablen kann Multikolinearitäten reduzieren. Ergebnisse einer entsprechenden Prozedur sind in Tabelle 9 gelistet.
|
Koeffizient |
Wert (kodiert) |
Wert (unkodiert) |
SE-C1) |
T-Wert |
P-Wert2) |
VIF3) |
|
1) Standardabweichungskoeffizient = Verhältnis Mittelwert/Standardabweichung 2) P > 0,05 insignifikant; P < 0,01 sehr signifikant; P < 0,001 extrem signifikant [5] 3) Variance Inflation Factor; soll den Wert VIF = 10 nicht überschreiten [9] 4) Standardabweichung |
||||||
|
a0 |
13,07 | -19,18 | 0,518 | 25,22 | 0,000 | – |
|
a1 (dN) |
2,21 | -0,374 | 0,304 | 7,26 | 0,000 | 1.06 |
|
a2 (p) |
0,865 | 5,38 | 0,304 | 2,84 | 0,009 | 1.06 |
|
a3 (wV) |
5,830 | 0,439 | 0,330 | 17,66 | 0,000 | 1.24 |
|
a6 (dN·wV) |
0,986 | -0,0034 | 0,305 | 3,23 | 0,003 | 1.01 |
|
a9 (wV·wV) |
-1,86 | 0,0263 | 0,443 | -4,19 | 0,000 | 1.28 |
|
S4) |
1,65 % | |||||
|
R2Adj |
92,89 % | |||||
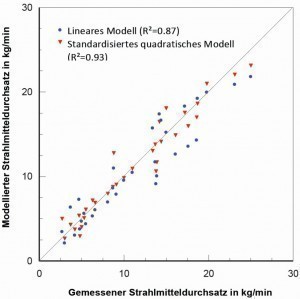Abb. 4: Korrelation zwischen mittels Regressionsmodellen ermittelten und gemessenen Strahlmitteldurchsätzen für das nichtmetallische Strahlmittel (Kupferhüttenschlacke)
Die deutlich reduzierte, aber genauere, modifizierte Regressionsgleichung ist in Gleichung <11> zu sehen. Standardabweichung und Regressionskoeffizient zeigten leicht verbesserte Werte. Die VIF-Werte waren deutlich reduziert (<<10) und hatten sich einem Idealwert von 1.0 angenähert. Es konnte weiterhin festgestellt werden, dass die Faktoren Düsendurchmesser und Ventilöffnungsgrad sowie die quadratische Interaktion vW*vW extrem signifikant waren. Diese Signifikanzen waren aufgrund der Multikolinearität verdeckt worden. Die weiter oben angedeutete Möglichkeit des Vorzeichenwechsels bei den Regressionskonstanten aufgrund von Multikolinearität wurde bestätigt. Ergebnisse der Regressionsrechnungen sind in Abbildung 4 gegen die gemessenen Werte für den Strahlmitteldurchsatz aufgetragen.
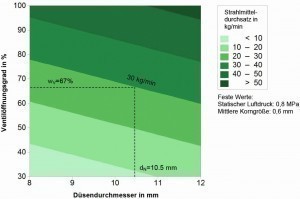Abb. 5: 2-dimensionale Simulation des Strahlmitteldurchsatzes für Stahlguss. Variable Kennwerte: Düsendurch- messer (dN in mm) und Ventilöffnung (wV in %); feste Kennwerte: statischer Luftdruck (p = 0,8 MPa) und mittlere Strahlmittelkorn- größe (dP = 0,6 mm). Beispiel: dN = 10,5 mm, wV = 67 % ®Strahlmitteldurchsatz = 30 kg/min
Zusammenfassung
Der Strahlmitteldurchsatz ist ein wichtiger Prozesskennwert beim Entschichten von Stahlsubstraten mittels Strahlen mit festen Strahlmitteln. Der Beitrag beschreibt statistische Untersuchungen zum Einfluss von vier Faktoren (Düsendurchmesser, statischer Luftdruck, Ventilöffnungsgrad und Strahlmittelkorngröße) auf den Strahlmitteldurchsatz zweier Strahlmittel (Kupferhüttenschlacke, Stahlguss). Einige Faktoren wiesen statistisch signifikante Einflüsse auf beide Strahlmitteltypen auf, während andere Faktoren statistisch insignifikant waren. Für beiden Strahlmitteltypen wurden Regressionsmodelle entwickelt, mit deren Hilfe sich Strahlmitteldurchsätze bestimmen ließen. Für Kupferhüttenschlacke erwies sich ein standardisiertes quadratisches Regressionsmodell als geeignet. Für den schwereren Stahlguss lieferte ein lineares 3-Parameter-Regressionsmodell hinreichend genaue Werte. Die Regressionsmodelle können verwendet werden, um optimale Werte für den Strahlmitteldurchsatz einzustellen, wofür in Abbildung 5 ein Beispiel abgebildet ist.
Danksagung
Die statistische Auswertung wurde von Dipl.-Ing. T. Marquardt, Muehlhan AG, Hamburg, durchgeführt.
Literatur
[1] Adlassing, K.; Jahn, W.: Die Eigenschaften von Strahlmitteln und Düsenwerkstoffen bei Druckluft-Strahlanlagen, Giesserei, 48 (1961) 618–622
[2] Bae, H.J.; Baek, J.J.; Lee, C.S.: Improvement of blasting productivity by optimizing blasting-related operation parameters, In: Conference PACE 2007, Dallas, TX, USA, 11.–14. Februar (2007)
[3] Beverloo, W.A.; Leniger, H.A.; van de Velde, J.: The flow of granular solids through orifices, Chemical Engineering Science, 15 (1961) 260–269
[4] Brauer, H.: Grundlagen der Einphasen- und Mehrphasenströmungen, Verlag Sauerländer, Aarau, 1971
[5] Garcia-Diaz, A.; Phillips, D.T.: Principles of Experimental Design and Analysis, Chapman & Hall, London, 1994
[6] Hareux, D.; Riac. B.: A comparative study of air blasting using different abrasives, Corrosion Protection Materials, 5(1), (1968) 18–34
[7] Holt, S.; Austin, D.M.: How nozzle pressure and feed rate affect productivity of dry abrasive blasting, Journal of Protective Coatings and Linings, 18(10), (2001) 82–104
[8] Kambham, K.; Sangameswaran, S.; Datar, S.R.; Kura, B.: Copper slag: optimization of productivity and consumption for cleaner production in dry abrasive blasting, Journal of Cleaner Production, 15 (2007) 465–473
[9] Kutner, M.H.; Nachtsheim, C.J.; Neter, J.: Applied Linear Regression Models, 4th ed., McGraw-Hill, Irwin, 2004
[10] Mellali, M.; Grimaud, A.; Fauchais, P.: Parameter controlling the sand-blasting substrates for plasma spraying, In: Proceedings 7th International Thermal Spray Conference, Boston, MS, USA, 20.–24. Juni (1994) 227–232
[11] Momber, A.W.: A generalized abrasive water jet cutting model, In: Proceedings of the 8th American Water Jet Conference, (1995) (ed. T.J. Labus), WJTA, St. Louis, Vol. 1, 359–371
[12] Momber, A.W.; Kovacevic. R.: Principles of Abrasive Water Jet Machining, Springer, London (1998)
[13] Momber, A.W.: Blast Cleaning Technology, Springer Publ., Heidelberg, (2008)
[14] Nadkarni, V.S.; Sharma, M.C.: Some aspects of mass flow control of shots in pneumatic systems, The Shot Peener, 10(3) (1996) 30–34
[15] Neelakantan, M.N.; Green, R.G.: The measurement and control of impact finishing processes, Journal of Physics E: Scientific Instruments, 15 (1982) 1332–1336
[16] Rawlings, J.O.; Pamtula, S.G.; Dickey, D.A.: Applied Regression Analysis: A Research Tool, 2nd ed., Springer, New York (1998)
[17] Remmelts, J.: Optimum conditions for blast cleaning of steel plate, British Corrosion Journal, 3(1968) 88–89
[18] Schulze, D.: Pulver und Schüttgüter (Chapter 12), Springer-Verlag, Berlin-Heidelberg (2009)
[19] Siebertz, K.; van Bebber, D.; Holzkirchen, T.: Statistische Versuchsplanung, Springer-Verlag, Berlin-Heidelberg (2010)
[20] Tanaka, T.; Kawai. S.: Ausfluß von Schüttgütern aus Bunkern mit einer vertikalen Wand und rechteckiger Auslauföffnung, Aufbereitungs-Technik, 4(7) (1963) 282–286
